Bilim insanları yeni bir şey ortaya atmak istediklerinde ne yapıyorlar? Bir konu hakkında rasyonel bir çözüm getirmek için hangi işlemlerden geçiyorlar? Ya da teori ve yasa nedir? Ya da teorinin kanundan (yasadan) farkı ne ve teori asılsız bir iddia mı? Matematik ile Bilimin farkı ne? Yani kısacası bilim nasıl çalışır? Hepsinin cevabı bu yazımızda, dilerseniz vakit harcamadan devam edelim.
İçindekiler
Teori ve Kanun: En Çok Karıştırılan İki Kavram
Bilimsel Bir Kanun (Yasa) Nedir?
Bilimsel bir kanunun ne olduğunu genel olarak biliriz. Buna en iyi örnek Newton’un hareket yasaları ve Kütle Çekim “kanunu”dur. Newton, hareket yasaları ile birlikte, matematiksel olarak, gözlemlediğimiz tüm nesnelerin uyduğu bir kaç denklem ve kural ortaya attı. Yani, denkleme bir kaç tane değer eklerseniz denklem size, mevcut nesnenin gerek şu an ve gerek gelecekteki halini verebilir. İşte bunlara kanun denir ve görüldüğü üzere kanunlar kesindir. Diğer bir örnek ise Newton’un kütle çekim yasasıdır. Kütle çekim yasası bize, iki cismin aralarındaki kütle çekimsel kuvvetin kütleleriyle orantılı ve uzaklıkların kareleriyle ters orantılı olduğunu söyler.
Görüleceği üzere, kütle çekim kanunu kesindir ve tüm gök cisimleri buna uyar; tıpkı biz insanların “yasalara” uyduğu gibi. Şimdi ise önemli kısma gelelim: dikkat ederseniz Newton, kütle çekim için herhangi bir mekanizma ortaya koymadı. Yani Newton, kütle çekimin nereden kaynaklandığını, gerçekten ne olduğunu gibi sorulara cevap vermedi. Daha açıklayıcı olması açısından elektromanyetizmayı ele alalım. Işığı düşünelim: ışık hakkında baya bir şeyler biliriz; tıpkı Newton’un kütle çekim hakkında bildiği gibi; fakat aynı zamanda ışığın nasıl çalıştığını ve ne olduğunu da biliriz.

Mesela, ışığın hem dalga, hem de parçacık olduğunu, farklı dalga boylarının farklı renkler ortaya çıkaracağını ve ‘Doppler etkisi’ gibi ışığın bize sunduğu efektleri de biliyoruz. Yani ışığın “mekanizmasını” biliyoruz. Newton ise kütle çekiminin kanunu hazırlamasına karşın ‘mekanizmasını’ sunmamıştı, bunun için yeni ‘teoriler’ gerekiyordu. Yani, Newton; trenin ne kadar hızlı gittiğini ve ne kadar kömür gerektirdiğini biliyordu fakat trenin nasıl çalıştığına dair kayda değer bir yorum getirememişti. İşte kütle çekimin, nasıl çalıştığını, ilerlediği, nereden kaynaklandığı gibi soruların cevaplarına ise hipotez denir. Eğer bu hipotezler, deney ve gözlemle kuvvetlendirildiğinde ise artık onlara teori denir; az sonraki bölümde bunu ayrıntılı olarak göreceğiz.
Fizik Kanunları Değişebilir Mi: İlginç Bir Soru
Kanunlar genelde kesindir ve değişmez deriz. Sonuçta bir kağıda yazılmış birkaç santimetrelik bir formül, gerçekten de dünyamızda işe yarıyor, uçaklar uçuyor; gezegenlerin hareketlerini de tahmin edebiliyoruz; o halde kanunların zaman içinde değişmesi gerçekten de zor. Fakat şu da ihmal edilmemelidir ki, kanunlarımızın; yarın çalışacağının hiçbir garantisi yoktur. Newton’un kütle çekim yasaları, bir gece tam tersi olabilir ve bunun olmaması için de hiçbir garanti yoktur. Birkaç önceki asra damga vuran filozoflardan biri Berkeley de şöyle bir soru sormuştu: “Kimsenin olmadığı ormanda düşen bir ağaç ses çıkarır mı?” Ormandaki ağacın ses çıkarması için hiçbir garanti yoktur. Aynı şekilde de yasaların çalışmaması için.
Peki ne yapıyoruz! Burada ince bir çizgi var. Bilim insanları, direkt olarak yasaların hep geçerli olacağını düşünüyor. Bunun nedeni ise felsefi bir konu olan Ockham’ın Usturası. Mesela, televizyon kumandasını kaybettiğinizi düşünün. Bu durumda olasılıklar şunlardır: Bir uzaylı kumandayı aldı götürdü, Biri; görünmez iken kumandayı aldı, kumanda uçtu vb. vb. Fakat Ockham’ın usturası burada devreye girer: bu fantastik olasılıkları bir usturayla kesip atıp yerine gayet gerçekçi ve basit senaryolar öngörmeliyiz. Baktığımızda da kumanda gerçekten koltuğun altına vb. girmiş olur. Yasalarda da aynı şekilde. Hiçbir günün, ertesi gününde yasaların değiştiği görülmedi! Aynı şekilde, binlerce yıllık yasaların, yarın değişebileceğini iddia etmek kadar durumu karmaşıklaştıran durum yoktur! O yüzden ise yasaların yarın değişebileceği ihtimalini, ustura ile kesip atarız. O halde, sonuç olarak ise elimizde yasaların kalıcılığı kalır.

ile meşhurdur.
-Teori ve Kanun arasındaki fark nedir?
Birkaç Bilimsel, Fiziksel Yasa Örneği
Bu bölümde birkaç kanun örneği görüp kanunların tam olarak neler olduğunu göreceğiz. Dilerseniz örneklerimize başlayalım:
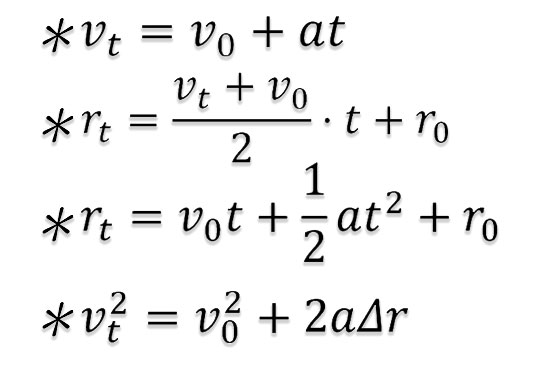
- Kinematik Denklemler: Sabit ivmeyle yani hız artışıyla hareket eden bir cismin, harekete başladıktan belli bir zaman sonra nerede ve hızın hangi durumda olduğunu merak ediyor musun? O zaman kinematik denklemleri kullanabilirsin. Kinematik denklemler bize sabit bir ivmeyle hareket eden bir cismin hareketinin belli bir zamanında kendisi hakkındaki birçok bilgiyi bize verir. Ayrıca kinematik denklemleri de türetmek çok kolaydır. Fakat kinematik denklemi bize, ancak bir cismin nasıl hareket ettiğini söylerler fakat bir cismin neden hareket ettiğini söylemezler. İşte burada ise devreye kuvvetler girer. Eğer bir cisim hareket ediyorsa orada hep kuvvetler vardır. En kötü ihtimal, cisim sabit hızdaysa bile o zaman cisim üzerinde dengelenmiş kuvvetler olabilir. İşte, cisimlerin neden hareket ettiği sorusuna da kuvvetler cevabı verilebilir. Yani, nasıl hareket ederler: Hareket denklemleri; neden hareket ederler: kuvvetler!
(Ek bir not: son yüzyıllarda kuvvet olmadan da hareket edilebileceği anlaşıldı. Fakat hareketin nedeninin kuvvet olması, klasik fizikte hep kullanabileceğimiz bir şey.)
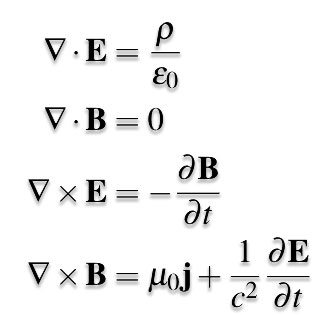
- Maxwell Denklemleri: Çoğu bilim insanının aklına, Elektromanyetizma denince Maxwell Denklemleri gelir. Maxwell Denklemleri, birkaç tane denklemin toplamıdır ve elektromanyetizmanın ana yasalarıdır. Bunun sonucunda ise Maxwell denklemleri, elektromanyetik olayların nasıl çalışacağını açıklar fakat dikkat ederseniz niye çalıştığını bize aktarmaz. Bunu bize aktaran şey, elektronların ve protonların incelenip, yüklerin nasıl etkileştiğidir. Mesela, akımın aslında hareket elektronlar olduğu söylenebilir. Çünkü elektronlar bunun için en uygun adaydırlar: hızlı hareket ederler ve protonları aksine atomdan daha kolay bir şekilde kopabilirler. Ayrıca, elektromanyetizmanın mekanizmasının tam olarak ne olduğu da sorulabilir. Neyse ki elektromanyetizma, bizi bu konuda kütle çekim kadar zorlamadı. (Aslında kütle çekim hala zorluyor!) Mesela iki mıknatıs alın ve zıt kutuplarını yaklaştırın. Yaklaştırınca anlayacaksınız ki sanki mıknatısların arasında “elektromanyetik bir alan” var ()Benzeri, bobinlerde de görülebilir) . Gerçekte de bu böyledir. İşte, bu da işin teori kısmıdır.
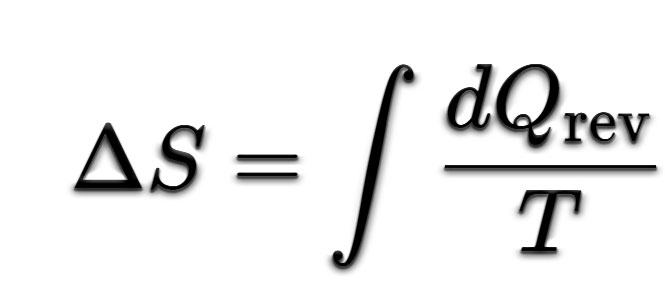
fiziksel evreni açıklamamız için
en önemli kavramlardan birisidir. Entropi Nedir?
- Termodinamik Yasaları: Termodinamik yasalar da, evrenimizde ısının, enerjinin hareketini betimler ve bunları ele alır. Maxwell denklemleri gibi Termodinamik yasaları da matematikseldir ve bize olayların nasıl gelişeceği hakkında kuvvetli öngörüler sağlar. Fakat gene bize, olayların “niye” böyle olduğunu açıklamaz. Bu durumda da teoriler devreye girer. Mesela ısı alışveriş aslında nedir? Termodinamik olarak ısı alışverişini analitik veya sayısal olarak çözebilirsiniz. Fakat buradaki soru şudur: Isı alışverişe tam olarak ne sebep olur? Sonra anlarız ki, moleküller devamlı titreşiyorlar ve bununla birlikte sürekli hareket halindeler. Bu şekilde de ısılarını etrafa yayıyorlar. Bu, makul bir hipotezdir fakat gözlemlenmelidir de!
Gördüğünüz üzere kanun örnekleri birbirine epey benzer ve aslında belli bir kalıptadırlar: Evrenimizdeki belli alanlardaki olayların nasıl süregeleceği, şu anki durumunu matematiksel olarak anlamamızı sağlarlar; fakat genelde bu olayların “asıl nedenlerini” belirtmezler. Şimdi ise sıra “asıl nedenlere” geliyor: Teoriler.
- Kütle çekim Yasası: Basit gibi görünen ama çok zor olan sorularla başlayalım: Dünya neden Güneş’in etrafında döner ve Dünya’nın yüzeyinden bırakılan elma neden dünyaya düşer? Elmanın düşmesini ve Dünya’nın Güneş etrafında dönmesini sağlayan şey nedir? İşte, bunlar 17. yüzyılda Isaac Newton’un aklına takılan sorulardı ve bunları cevaplamak için kuramlar geliştirmeyi düşünüyordu. Isaac Newton, bu soruların cevabını kütle çekim olarak verdi. Her kütle başka kütleyi çekiyordu. Kütle Çekim teorisi ve yasası bu soruların cevabı oldu. Fakat kütle çekimin teorisinin teorisi eksik kaldı. Mesela kütle çekimin anlık etki etmesi, Newton gibileri rahatsız ediyordu. Diğer bir soru ise kütle çekimin gerçekten ne olduğuydu. Newton, kütle çekimi kuvvet olarak kabul etmişti fakat bunun yanlış olduğu Einstein’ın yeni kuramlarıyla anlaşıldı.
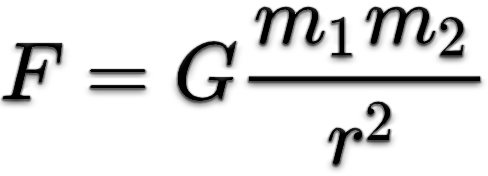
Bilimsel Bir Teori veya Bir Hipotez Nedir?
Önceki bölümde bilimsel bir kanunun ne olduğunu görmüş ve ilk olarak hipotezin sonra ise teorinin ne olduğuna dair ufak ipuçları kazanmıştık. Şimdi ise hipotezin, ardından ise hemen sonra teorinin ne demek olduğuna dalalım. Kanunlar, fiziksel bir olayın -mesela matematik ile- açıklanmasıdır. Fakat kanunlar genelde fiziksel olguların arka planını açıklamazlar; çünkü genelde olayın arka planı, olayların gidişatını anlamaktan daha zordur. Mesela, yörüngelerin elips oluşunu anlamak bir nebze kolaydır, çünkü her gece dikkatli gözlemlerle bunu görebilirsiniz; fakat gezegenlerin neden elips olduğunu evren bize sunmaz; onu dikkatlice aramamız gerekir.
İşte, bu arayış sürecindeki ortaya attığımız cevaplara hipotez denir. Eğer bu hipotez, deney ve gözlem (ve matematik ile de!) ile desteklenirse artık bu cevaba teori denir ve kısacası her bir teori ise olayların arka planını açıklamaya çalışır. Mesela atom teoriler, maddenin en küçük yapı taşını betimlemek için ortaya atılan teorilerdir. Şimdi de dilerseniz az önceki yörüngelerin elips olması örneğine dönelim, gezegenlerin elips olmalarının nedeni, Newton yasalarından gelmektedir; yani Newton’un kanunları, yörüngeleri elips öngörür. Yani, teoriler; kanunların yardımıyla da keşfedilebilir sonuçta Einstein bile ışığın ve elektrodinamik dalgaların hareketli cisimler üzerindeki etkileri (Electrodynamics on Moving Bodies) hakkında makale yazarken Maxwell’in “Yasalarını” göz önüne almıştı ve teorisini onunla ilerletmişti. Ayrıca her teori ve hipotez, yanlışlanma kabiliyetine sahiptir, eğer teorinin aksine bir tane bulgu keşfedilirse o halde teori ya değiştirilir veya çöpe atılıp yeni teorilerin gerekliliği ortaya çıkar. Ayrıca az sonra göreceğimiz üzere teoriler; asılsız, geçersiz, kanıtlanmamış şeyler değillerdir aksine büyük bir filtreden geçerler. Zaten burada da iyi ve kötü teorinin ayrımı yapılmış olur. Ufak bir başlığa daha göz atıp hemen örneklere geçelim.
Bilimde İyi Bir Teori Nedir ve Nasıl Olur?
İyi bir teori, sadece bize olayın arka planını sunmakla kalmayıp; ayrıca bu teori doğruysa belirli öngörülerde bulunmalıdır. Bunun iki sebebi vardır; birincisi insanlık olarak bilimdeki ana amacımız doğrultusundaki evreni anlama ufkumuz genişler, ikincisi bu ön görüler; teorinin kanıtlanması için gözlemlenebilir kanıt olanağı sunarlar. Nitekim, bir bilimsel teori ne kadar zarif ve güzelse de eğer bilimsel bir teori, gözlemsel olarak kanıtlanmazsa o teori kanıtlanmış sayılmaz. Yani bu kısım çok önemli.
Ayrıca, öngörüler; teorinin teorik olarak kanıtlanmasına da yardım eder. Çünkü, düşünün ki; teorinin ön görüleri, şu anki fizik bilgimizle çelişiyor olsun. Eğer bu yanlış çok barizse büyük ihtimal teori hatalıdır. Bu yöntem iyidir, çünkü gözlemlenebilir bir kanıta gerek kalmaz. Çünkü önceki fizik teorileri ve kanunları kanıtlanmış olduğu için bunlarla barizce çelişen öngörüler, büyük ihtimal hatalıdır. Fakat bu yanlış, bizim önceki fizik kanunları hakkındaki cahilliğimizden kaynaklana da bilir. İllaki de önceki fizik bilgilerimiz de hatalı olabilir. Bu da kendi anlayışımızı sorgulatır, fakat dikkatli olunmalıdır.

Mesela 1900’lerin başında klasik fizikte çok büyük bir problem olduğu keşfedildi: Eğer o günkü klasik fizik kullanılarak bir kara cismin (başka bir değişle kendisine yansıyan ışığın hepsini emen ideal bir cisim) keyfice herhangi bir enerji seviyesinde ışınım yaptığı kanıtlanabilirdi. Bu, çok büyük bir sıkıntıydı. Şayet bu olsaydı bir sıcak bir kahve dolu fincan yüzünden amansız bir hastalık olan kansere yakalanabilirdiniz! Sonuç olarak önümüzde iki seçenek vardı: Birincisi Klasik Fiziği çöpe atmak (ki bu çok saçma olurdu!), ikincisi ise klasik fiziği düzeltmek. İkincisini uygulamaya çalıştık ve iyi bir sonuç verdi. Dikkat ederseniz bu problem, herhangi bir deneysel bir olay öngörmedi; öngördüğü şey, teorikti. Ve bu teori gerçekten de çelişkiliydi. Bu örnekten sonra yani şimdi ise metolojiden çıkıp daha eğlenceli olan örneklere geçiyoruz:
Bilimde Teori Örnekleri
Kütle Çekimi Anlamak İçin İlk Teori
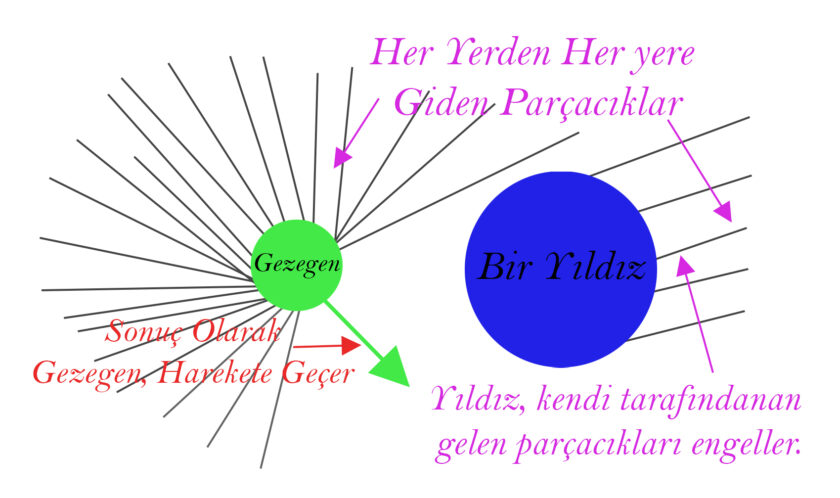
Önceki bölümlerden de görüleceği üzere Newton, kütçe çekimi hakkındaki derin sorulara cevap vermedi: “Kütle Çekim nereden geliyor, nasıl yayılıyor, kütle çekim sonsuz hızda her yeri etkiliyor mu yoksa belirli bir hızda mı?”. Bu soruların cevaplara yani teorilere ihtiyacı vardı ve ilk girişim geldi. Dilerseniz bu örneğimize geçelim. Bu hipotez (az sonra teori olacak), uzayın her yerinden her yerine giden parçacıklar olduğunu varsaymıştı. Bunların da gök cisimlerine çarpması, gök cisimlerine yön veriyordu. Eğer cismin her yerinde eşit olarak parçacık çarparsa o zaman cisim hareketsiz durur. Fakat eğer cismin yakınında büyük bir gök cismi varsa ne olur? Şayet o zaman, aslında gezegene çarpmış olacak parçacıklar o gök cismi (mesela Güneş) tarafından engellenir ve gezegen o gök cismine göre sürüklenmeye başlar. Çünkü sonuçta, diğer yönlerden parçacık çarpmaya devam eder fakat öteki tarafta bunları dengeleyecek bir kuvvet olmadığı için gezegen, büyük gök cismine doğru harekete geçer. Bu böyle devam eder ve gezegen, gök cismi etrafında döner.
Evet, gayet makul bir teori; muhtelemen gözlemlenebilir. Ayrıca aynı teori, Jüpiter gibi büyük gezegenlerin de parçacıkları engellemesi ile Dünya’yı çekmesini açıklıyor; o yüzden teori gerçekten de kuvvetli. Bu gibi destekleyici unsurlardan dolayı bu hipoteze artık teori diyebiliriz. Fakat her teori dışarıdan göründüğü gibi güçlü olmayabilir şimdi ise bu teorinin nasıl çürütüldüğünü anlatacağız.
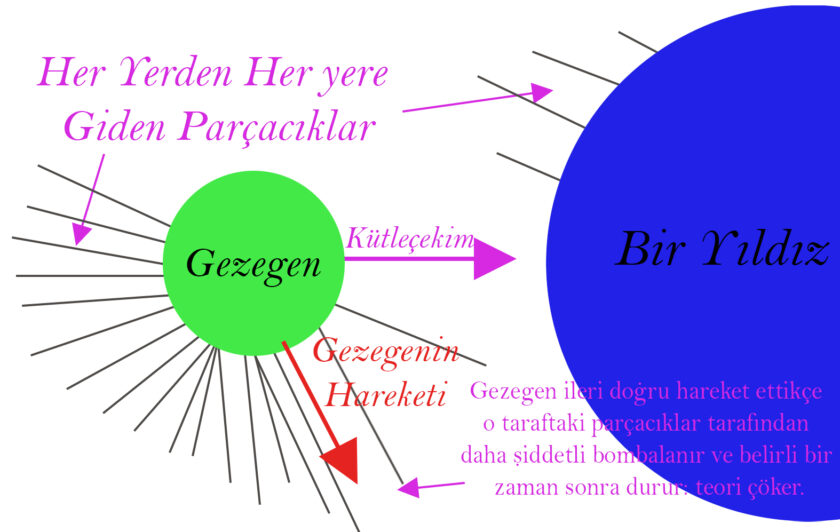
İlk Girişim Başarısızlık İle Sonuçlanıyor
Bu teori girişiminde çok büyük bir hata var. Dünya’nın Güneş’in etrafında döndüğünü düşünelim. Bu durumda Dünyanın dönme eksenin zıt yönde Dünya’ya çarpan parçacıklar açık ki, diğer taraflardan çarpan parçacıklardan daha güçlü bir şekilde çarpar ve Dünya’yı zamanla durdurur. Bunu yağmurlu vakitlerde arabayla giderken de yaşarız. Hızlandıkça yağmur damlaları çok daha sert çarpar ve aslında arabamızı (Bizim deneyimizde Dünya’yı) durdurur. Fakat arabamızın, motoru vardır ve bu karşı kuvvete karşı gelebilir. Fakat Dünya’da böyle bir mekanizma olduğu için Dünya’nın bir süre sonra durması gerekirdi! Fakat bu kesinlikle ama kesinlikle yanlış bir sonuç! On yıllar boyunca hiç bir zaman Dünya’nın durduğunu görmedik! Bu yüzden bu teoride bir sıkıntı olduğu anlaşıldı, iki seçenek vardı: Ya teori düzeltilecek, ya da teori çöpe atılacak! Birincisinin işe yarama ihtimali çok düşük, çünkü teorideki problem; problemin ana varsayımında bulunuyor. O yüzden mecburen bu teoriyi çöpe atıp yeni birini aramaya başlamalıyız.
Ayrıca bu teori bir şeyi daha atlar: teoride, kütle çekiminin ana sebebi kütle (ya da enerji) değildir. Sonuçta burada önemli olan, bir gök cisminin yüzey alanıdır. Buradan da bir yıldızın yüzey alanı ne kadar büyük olursa o kadar çok kütle çekimi uygulayacağı çıkar. Fakat bu da deneylerimizle pek uyuşmamaktadır. Mesela, çapının (Yani aslında yüzey alanının) küçüklüğüne karşın normal yıldızlardan çok daha kütleli olduğu bilinen bir Nötron yıldızı tam bir kütle çekim devidir. Fakat hemen yukarıdaki teoriye göre bunların başka cisimlere uyguladıkları kütle çekim kuvveti daha az olmalıdır. İşte burada da gözlemle çelişir. Sonuç olarak, bu teoriyi atmalıyız. Size az önce, bir teorinin hangi aşamalardan geçtiğini anlattık. Fakat gerçek bundan da öte. Bir teori sadece birkaç testten değil, aksine bağımsız kişiler tarafından kurgulanan bir çok gözlemden geçirilir. Bu da çok güçlü bir filtredir.
Genel Görelilik Kuramı: Einstein, Kütle Çekim Sorusunu Çözüyor!
Yıllar 1915’i gösterdiğinde Albert Einstein, görelilik kuramını ortaya attı ve bu “teorisinde” kütle çekimin nasıl yayıldığına, neyden kaynaklandığıyla alakalı sorulara cevap verdi. İşte bu, kütle çekimin teorisi oldu. Kütle çekim, Newton’un düşündüğü gibi bir kuvvet değil; aslında uzay zamandaki bükülmelerdi.
Bir bilyenin çukurlarda yuvarlanması gibi kütleler de bükülmüş uzay zaman içinde kütle çekim dediğimiz sonuca maruz kalıyorlardı. Ayrıca Einstein’ın Görelilik Kuramı, birkaç tane öngörüde bulundu. Bunlardan biri ise o günkü şartlar altında gözlemlenebilirdi: Işığın Kütlenin Etrafında Bükülmesi. Yani ışık da kütle çekiminden etkileniyordu aslında. Yani ışık, büyük kütlelerin yanında birazcık da olsa sapmalıydı. Bunun sonucunda ise 1919’da bu öngörünün ispatlanması sonucu Görelilik Kuramının doğruluğu ilk defa açığa çıkmış oldu.
Sonraki yıllarda ise gerek başka öngörülerle daha hassas ölçümler yapıldı ve her defasında Görelilik Kuramının öngördüğü şeyler yüksek doğrulukla kanıtlandı ve kuram her bir kanıtta güç kazandı. Fakat Genel Görelilik Kuramı, bir “teori” olduğu için genel bildiğimiz anlamda, asılsız, gerçek dışı vb. gibi algılanmamalıdır. Aksine Genel Görelilik Kuramı gibi bir sürü teori, zor ve uzun süzgeçlerden geçmişlerdir. Buradan da aslında teorilerin güçsüz ve asılsız şeyler olmadığını aksine çok uzun süzgeçlerden geçtiklerini görüyoruz.

Licence: CC BY-SA 3.0
Genel Görelilik Kuramı’na Yardım Etmemiz Gerek!
Her ne kadar başarılı da olsa görelilik Kuramının açıklamakta çok zorlandığı ve bazen açıklayamadığı olgular var. Mesela Kara Delikler bunlara örnek. Kara Delik tekilliğinde uzay zaman, yoğunluğu devasa büyüklükte (sonsuz denilebilir!) olan bir noktaya sıkışır ve çok güçlü bir kütle çekim alanı oluşturur. Genel görelilik ve çoğu teori, uzayın az bir kıvrımı veya tamamen düz olduğunu varsayar. Fakat tekillikte uzay zaman bükülmesi sonsuzdur (O ne demekse!)! Sonuç olarak Genel Görelilik denklemleri ve tabi ki de klasik fizik burada çöker ve kullanılamaz hale gelir.
Bir teoride eksikler çıkarsa genelde +şunlar yapılır: Ya teori çöpe atılır, teoriye eklemeler yapılır ya da destekleyici teoriler geliştirilir. Genel Görelilik kuramını çöpe atacak halimiz yok; çünkü halihazırda teori çok başarılı ve evrenimizin büyük çoğunluğunda uygulanabilir. O halde, Genel Görelilik Kuramına ya ekleme yapmalıyız veya buna destek çıkan farklı bir teori ve alan geliştirmeliyiz. Biz ekleme yapmayı seçiyoruz. Çünkü geliştirdiğimiz teori büyük ihtimalle genel görelilik ile bağlantılı olacak. İşte buna da Kuantum-Kütle Çekimi diyoruz.
Bunun, alanlarında en başarılı teoriler olan Kuantum teorisi ve Genel Görelilik kuramını birleştirmeyle olacağını düşünüyoruz. Kuantum teorisi, büyük şeyleri açıklamazken; Genel Görelilik kuramı, küçük şeyleri açıklayamaz. Bu ikisini birleştirmek, hem küçük düzeyde hem de büyük düzeyde kütçe çekimi uygulamamızı sağlayacak. Fakat bu çok zor. Fakat başarılı teoriler üretmenin kolay olacağını kim söyledi? Fakat teoriler üretip, yanılıp bunu başaracağız.

Nebular Teori: Güneş Sistemi Nasıl Oluştu

Güneş sistemini tabi ki de çok iyi bir şekilde açıklayabiliyoruz. Fakat ya geçmişini? Güneş Sistemi’nin tabi ki de geçmişini klasik fizikle “doğrudan” göremiyoruz. Bunun nedeni birçok faktör olması ve bazı faktörleri bilmememiz. Fakat işte burada devreye teoriler giriyor. İlk başta Yüzlerce gözlemevi ve gözlemci Güneş Sistemindeki cisimleri inceler ve hangi cisimde hangi elementlerin olduğunu tayfölçer ile saptar. Bunun sonucunda da Güneş Sistemi’nin geçmişinde hangi elementlerin daha çok olduğu, ne tür bir yıldız patlamasının gerçekleştiği gibi sürü soruya cevap verebiliriz. Bu süreçte ise teorik fiziği de dikkate alırız ve elimize kapsamlı bir teori ortaya çıkar. İşte, bu; Nebular Teori. Nebular Teori, halihazırda kendi Güneş Sistemimizi iyi bir şekilde betimlemekle kalmıyor aynı zamanda derin uzayda gördüğümüz Güneş Sistemi benzeri yapılarına iyi bir şekilde betimliyor. Bu yüzden Nebular Teori, güçlü bir teori. Ayrıca burada ise Nebular Teori’nin yasalardan da faydalanarak inşa edildiğini de ekleyebiliriz; bunu da ilk bölümlerde görmüştük.
Karanlık Enerji: Evren Neden Gittikçe Hızlı bir şekilde Genişliyor?
Hubble ile başlayan ve evrenin gidişatı hakkındaki maceramızın en önemli kilometre taşlarında birisi, evrenin gittikçe artan hızlarda genişlemesidir. Bu bulgu, bizi çok şaşırttı. Çünkü düşünürseniz, kütle çekim; evrendeki her bir şeyi birbirine daha yakın yapmaya daha doğrusu evreni küçültmeye çalışırken gizli bir şey, evrenin bunun aksine, genişlemesini sağlıyor. Ayrıca bu genişleme hızı, gittikçe artıyor. Fakat buna ne sebep veriyor? İşte büyük soru bu. Bu sorunun cevabını ancak çok az biliyoruz: karanlık enerji.
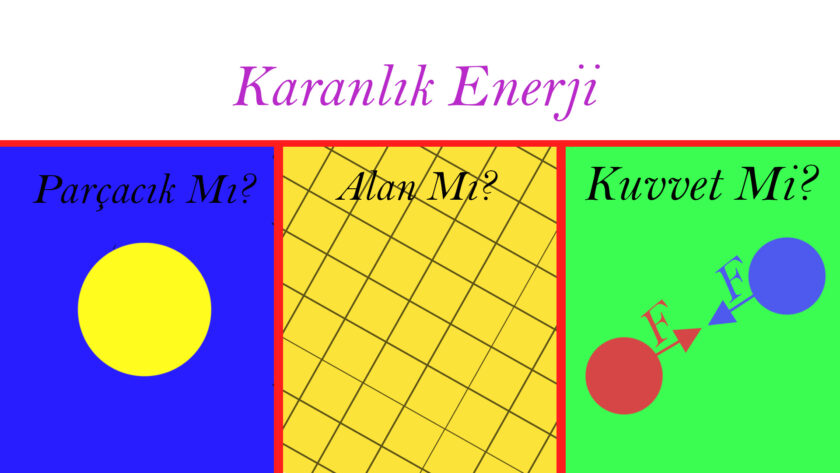
Karanlık enerjinin fotonlar gibi bir parçacık mı, güçlü nükleer etkileşim gibi bir kuvvet mi yoksa Higgs Alanı gibi bir alan mı olup olmadığını bilmiyoruz. Karanlık enerji hala bir hipotezdir ve teori olamamıştır. Çünkü karanlık enerji öyle gizemlidir ki, ışıkla veya bildiğimiz şeylerle, bildiğimiz kadarıyla, temasa geçmez. Bu yüzden de üzerinde bir deney yapmak çok zordur. Evet, şu ana kadar CERN ve dünyanın farklı noktalarındaki Hadron Çarpıştırıcılarında karanlık enerji gibi davranan garip bir şeye rastlamadık. Fakat bu, karanlık enerjinin yokluğu kanıtlamaktan ziyade onun gözlemlenmesinin çok zor olduğunu kanıtlıyor.
Buradaki farklı bir yaklaşım, karanlık enerjiye teorik olarak yaklaşıp; gözlemlenebilir ön görüler ortaya koymak olabilir. Fakat dediğimiz gibi kimse, bu konuda kayda değer bir ilerleme yapamadı. Böylece hala, evrenin bu garip genişleme özelliğinin nereden geldiğini çözmüş değiliz. Bunun için farklı teoriler ortaya atmak gerekebilir. Başarılı bir teori her yerden gelebilir ve bunun için her zaman teori üretip bunları sınamalıyız. Şimdi ise bilimin nasıl çalıştığına dair birkaç şey anlatacağız. İyi okumalar.
Bilim Nasıl Çalışır?
Meraklı bir fizikçisiniz ve evrenin doğasını merak ediyorsunuz. Bir şeyler yapmak istiyorsunuz ve yola koyuluyorsunuz. İki yolunuz var, birincisi bir soruna çözüm bulmak; diğeri ise doğadaki, üzerine daha önce kuvvetli bir teori kurulamamış olayı açıklayamaya çalışmak. İlkinden başlayalım. Eğer bir yerde bir sorun varsa ve bu açıklanamıyorsa bunun nedeni, büyük ihtimal, şu anki kuramlarımızın bu şey için iyi çalışmadığı veya yanlış olduklarıdır. Bu durumda yapabileceğimiz en iyi şey, yeni bir kuram icat etmektir. Fakat bu kuram tabi ki de önceki kuramdan farklı olmalı, öbür türlü ne anlamı kalırdı? O yüzden işe ilk önce tahminle veya bir kabul ile başlanmalı, öbür türlü yeni kuramı hiçbir şeyin üstüne inşa edemezsiniz; ve ekstra bir tahmin veya kabul ile başlanmadıkça yeni bir şey bulunması çok zordur.
Fakat bu kısım belki de çok zordur. En baştan kabulünüz yanlış olabilir, böyle bir ihtimal vardır; bu yüzden her zaman kuşkulu olmalı ve dışarıdan gelecek fikirlere de açık gözlü olmalısınız. Diyelim bir şeyleri kabul ettiniz ve devam ediyorsunuz; bu kabuller size yeni pencereler açar ve -eğer kuram gözlenebilir ise- gözlemlenebilir öngörüler sunar. Bunlar sayesinde de kuram doğrulanabilir. Buna bir örnek vermek gerekirse Görelilik Teorisini verebiliriz. 1900’lerin başında ışık hızı ve zaman hakkında bir sürü paradoks vardı ve ortada bir sorun olduğu barizdi. Maxwell, ışık dahil tüm elektromanyetik dalgaların sabit bir hızda ilerlemelerini gerektiğini söylemişti. Fakat bu bir paradoks olarak nitelendiriliyordu çünkü sonuçları ve tabi ki de kendisi, gerçekten garipti ve bunun böyle olacağı pek düşünülmüyordu. Bunun üzerine Einstein, görelilik hakkında çalışmalarını yaparken ilk olarak ışığın sabit bir hızda ilerlediğini varsayımını yapmış, sonrasında ise buna dayanarak baştan aşağı bir kuram inşa etmiştir. Einstein’ın da hesapladığı öngörüler yüksek doğruluk payı ile de yıllar içerisinde teker teker doğrulanmıştır. Aslında bu da ışığın sabit ve Maxwell’in Elektromanyetizma Kuramının doğru olduğuna dair dair de dolaylı kanıtlar sunmuştur.

Ayrıca tahmin etmenin de yararları olduğunu görürüz. Günlük hayatta olduğu gibi fizikte de sezgilerimiz vardır ve bunlar sayesinde fizikte de eşitlikleri veya kuramları tahmin edebiliriz. Mesela Bazı fizikçiler de vardır ki hayali bir senaryo kurarak büyük bir kuram inşa ederler. Mesela Maxwell. Maxwell’e kadar bazı elektromanyetik denklemler birbiriyle çelişiyordu ve bunlarda değişikliğe gidilmesi ihtiyacı vardı. Maxwell ise bu değişikliği nasıl yaptı dersiniz? Bir varsayımla başlamadı, direkt olarak denklemleri tahmin etmedi; onun yerine uzayda varsayımsal yani hipotetik avara çarkları hayal etti (Evet, Uzayda hayali avara çarkları). Maxwell’in bu düşünce deneyinin bugün yanlış olduğunu biliyoruz. Maxwell, aslında bir bakıma denklemleri hayal etmişti; fakat Maxwell’in hayali asılsız değil, aksine akla dayanan bir hayaldi. Yani Maxwell’in bu tahmini kesinlikle baştan savma değildi ve gerçekten de işe yaradı! Bugün Maxwell denklemleri büyük derece de önemlidir. Bunu da Maxwell’in olağanüstü hayal gücüne borçluyuz. Buna benzer bir şekilde de Schrödinger de kendi adıyla bilinen ve kuantum teorisi için çok önemli bir denklemi tahmin etti. Fakat gene, bu devrik bir tahmin değil, aksine “akıllı” bir tahmindi.
İkinci olarak ise bir şeyleri anlamak istiyorsanız da gene bir yerlerden başlamak ve düşüncelerinizi en basit bir temele dayandırabilmek için kabullere ihtiyacınız vardır. Mesela, Newton’un hareketin üç temel yasası buna örnek olabilir. Keza bu üç yasayı kullanarak kuvvet dediğimiz şeyi, klasik fizikte betimleyebiliriz. Ayrıca bulduğunuz sonuçlara da hemen atlamamalısınız, içinizde her zaman bir kuşku olmalıdır. Çünkü doğa yasaları bazen yanıltıcı olabilmektedir.
Bilim ile Matematiğin Farkı
Bilim ve Matematik birbiriyle iki çok yakın daldır fakat birbirlerinden bazı konularda uzaklaşırlar. Dilerseniz zaman kaybetmeden geçelim.
İlk olarak, bilimde bolca deney ve gözlem vardır. En soyut kuramlar bile gözlem ile kanıtlanmaya çalışılır. Oysa matematikte buna gerek yoktur; yaptığınız her şey zihinseldir. Matematikte bir sürü mantıksal zincir ile yeni şeyler öne süreriz. Bunların doğruluğunu da, önceki türettiğimiz şeyler ile kontrol ederiz. Fakat matematikte bu yüzden, aksiyom dediğimiz ilk mantıksal argümanlar bulunmalıdır. Eğer bu olmazsa mantıksal zinciri daha ilk baştan kuramayız.
Fakat biraz dikkatle bakarsak fizikte de varsayımlar kullanabiliyoruz. Mesela ünlü fizikçi Stephan Hawking’in birkaç konuşmasında veya kitabında (hatta filminde!) şunu görebilirsiniz: “Eğer Genel Görelilik Kuramı doğruysa (…)“ Buradaki “Eğer Genel Görelilik Kuramı doğruysa” sözü, bir varsayımdır. Burada bu varsayım, aslında gerçekçidir. Nitekim Genel Görelilik Kuramı, epey güçlü bir kuram. Bazı varsayımlar da daha da gerçekçidir: Ünlü Matematikçi ve Fizikçi Roger Penrose, kütlesi; belli bir kütleden büyük olan bir yıldızın, sadece “Kütle Çekiminin Çekici olması” varsayımını kullanarak bir tekilliğe çökeceğini kanıtladı. Mesela buradaki varsayım da çok basittir fakat böyle varsayımlar hesaplarımızda kesinlik kazanır ve çok önemli bir forma bürünürler. Benzer şekilde matematiksel ispatlarda da “$n>7$ olsun” yazdığını görebilirsiniz. Bunun sebebi, aynı şekilde bazen hesaplarımızın kesinlik kazanmasıdır.
Ayrıca bilimde de aksiyomlar vardır. İlk olarak Kepler’in 2. Yasası olan eşit alanlar yasasına bakalım. Bu yasaya göre Güneş etrafında dönen gezegenler, yörüngede eşit zamanda eşit alanlar tarar. Bunu bir aksiyom olarak alabilirsiniz, nitekim buradan ise matematikte olduğunu gibi farklı alanlara girebilirsiniz. Fakat kısa bir süre sonra anlaşıldı ki Kepler’in Eşit Alanlar yasası, doğrudan Newton’un icat ettiği Kütle Çekim kanununun bir sonucu. Yani aslında Newton’un kütle çekim kanunu bir aksiyom olarak alabiliriz. Fakat bundan daha iyisi de yaparak Newton’un geliştirdiği mekaniğin üç temel yasasını (Eylemsizlik, $\vec{F} = m\vec{v}$ ve her uygulanan kuvvete karşı, yönü zıt ama büyüklüğü eşit kuvvet vardır) aksiyom olarak alırız. Eğer bunları aksiyom olarak alırsak bir sürü şeye varabiliriz. Aynı matematikteki gibi aslında, fakat bolca deney var!

Sonuç olarak bilimdeki ana amacımız, evrene, doğaya bir açıklama getirebilmek. Bu yüzden ise deneysel gözlemler, çok önemli. Sonuçta ünlü fizikçi Feynman’ın da dediği gibi “Teorinizin ne kadar zarif ve güzel olduğu veya ne kadar zeki olduğunuz önemli değildir. Eğer teoriniz deneyler ile uyuşmuyorsa o zaman yanlıştır“ Bu yüzden bilimde deneysel kanıtlar çok önemlidir. Kafanızda sadece elindekilerle kara delikleri çözümleyemezsiniz, gözlem de gereklidir. Fakat matematikte kanıtlarımızı, ilerlememizi zihnimizle ve mantıksal örgülerle yaparız. Bu yüzden ise bir matematiksel teorinin gerçek ile alakası olmasa bile o alanda iyi bir şekilde ilerleyebiliyoruz.
Ayrıca matematikte bir şeylerin ne olacağını gene biz, insanlar belirleriz. Fizikte bunu yaparken doğaya bir ölçüde sadık kalmalısınız. Mesela kütle çekimin çekici olduğu, az çok bellidir. Fakat mesela matematikte bir tartışma konusu olan $0!=1$ (!, yani faktöriyel o sayıya kadar olan bütün sayıların çarpımıdır) gibi bir eşitliliğin doğru olup olmaması gerektiği için doğadan gelen bir referansımız, pekala; varsa bile çok azdır. Bunu kendimiz belirlemeliyiz. Fakat mesela, Heisenberg Belirsizlik İlkesini veya daha basitinden sıvıların sıkıştırılamama özelliğini sadece kendimiz ortaya çıkaramayız; çünkü bu doğrudan zihnimizin değil doğanın bir özelliğidir. Bunu, ancak gözlem yaparak anlarız, fakat dediğimiz gibi matematikte böyle bir zorunluluk yoktur. Ayrıca şunu da belirtmeliyim ki, fizik matematikten veya matematik de fizikten iyi değildir. İkisi en iyi dostlar gibidir; ikisinin de birbirine yardım ettiği bolca zaman olur fakat kesinlikle biri birinden üstün değildir. Bunu, itfaiye ile polis gibi de düşünebilirsiniz, kesinlikle polisin veya itfaiyenin birbirinden üstün olduğunu iddia edemezsiniz; işin aslı birbirlerine çok yardım ederler.
Bilimsel Bakış Açısı ve Matematiksel Bakış Açısı için bir Örnek
Gelin bir örnek üzerinden de bilimsel bakış açısını ve matematiksel bakış açışını karşılaştıralım. Bir satranç tahtası düşünün, bu satranç tahtasının karşılıklı iki köşedeki siyah taşı çıkartalım. O zaman şekil şöyle olur:

Problemimiz şu: Kalan satranç tahtasını; hiçbir taş boş kalmayacak şekilde her biri iki taşlık yer kaplayan ve sadece yatay ve dikey olarak yerleştirebileceğimiz domino taşları yerleştirebilir miyiz? Bu probleme ilk önce bir şans tanıyabilirsiniz. Ama biz devam edelim ve iki farklı bakış açısına bakalım.
- Bilimsel Bakış Açısı: Bir fizikçi böyle bir problemi çözmek isterse ilk olarak şöyle yapar: domino taşlarını birkaç kere yerleştirmeyi dener. Yani “deney” yapar. Baktı ki hiç olmuyor o zaman problemin çözümünü deneysel olarak “hayır, olmuyor” diye bulur. Fakat bu sonuç, başka bir deneyle saptırılabilir. Dediğim gibi hiç taş kalmayacak şekilde domino taşı yerleştirebildiğimiz bir oyun bile olsa cevap, tam tersi olurdu.
- Matematiksel Bakış Açısı: Bahsettiğim gibi bir matematikçi, bu oyunu çözerken daha çok mantıksal yapı ve rasyonel argümanlar kullanır. Şunu dinleyin: her yerleştirdiğimiz domino siyah ve beyaz kareleri kaplayacaktır. Yani her yerleştireceğimiz domino için boş bir siyah ve beyaz kare gerekir. Satranç tahtasında 32 siyah, 32 kare vardır. İki tane siyahı çıkardığımızda göre 30 siyah, 32 beyaz olur. Şimdi dominolarımızı yerleştirelim; 30 tane domino taşı yerleştirebiliriz, çünkü 30 tane siyah beyaz çift var. Fakat sonuçta iki tane beyaz kare kalır. İki beyaz kareye de domino taşı yerleştiremeyeceğimize göre dominolarla bu tahtayı kaplayamayız.
Buradan sonuç çıkartacak olursak, matematiksel kanıtların evrensel olduğunu görürüz. Hangi evrende (Düzlemde paralellik aksiyomu olursa güzel olur!) satranç tahtası çizerseniz çizin sonuç yine aynı olur. Fakat bilimsel bakış açısında kesinlik yoktur, olay deney gözleme bağlıdır. Aksini gösteren en az bir tane deney ve başka bir olgu olmadıkça doğruluğu devam eder. Ayrıca fizik kanunları, farklı bir evrende olağanüstü derecede farklı olabilir. Fakat eğer başka bir evrende sadece paralellik aksiyomu doğruysa Öklid’in Geometrisinin büyük oranını baştan aşağı inşa edebilirsiniz.
Matematikte Teori, Teorem, Aksiyom
Matematiğin bilimden bir diğer farkı da teorinin anlamının farklı olmasıdır. Matematikte teoriyi pek kullanmayız. Onun yerine “önerme” sözcüğünü kullanırız. Ve bu önerme dediğimiz şey illaki kabul görmesi gereken bir şey değil, tamamen zırva bir şey de olabilir. Adı üstünde “önerme”.
Mesela bir örnek verelim. Aklıma şöyle bir eşitsizlik gelmiş olsun: ikiden büyük her \(x\) için \(2^x\gt2x\) olur. Bu bir önermedir, sadece “öneriyorum”. Bunu ispatlayabilirim. Ama bir kanıtı bulunana kadar bu sadece bir “önermedir”.
Teorem ise kanıtlanmış önermeler için kullandığımız bir kavramdır. Mesela üstteki önermeyi kanıtlarsam “ikiden büyük her \(x\) için \(2^x\gt2x\) olur.” önermesi bir teorem olmuş olur.
Aksiyoma bakacak olursak aksiyom, matematiğin kanıtlanması gerekmeyen kabul görmüş kurallarıdır. Mesela \(a*b=b*a\) ifadesi bir aksiyomdur. Kanıtlanması gerekmez. Hilbert gibi bazı matematikçiler 19. yüzyılın sonlarında 20. yüzyılın başlarında matematiği aksiyomlaştırmaya giriştiler.

Bunun nedeni matematiksel çalışmaların artması ve bunun sonucunda ortak bir temel ortaya çıkarılması gerektiğiydi. Öbür türlü mesela bir matematikçi kanıt yapsa, neye göre yaptı? Nasıl yaptı? Hey bunu kullanamazsın, neye göre kullandın? Soruları ortaya çıkar. Bu da istemediğimiz bir şey tabi ki de. Yani aksiyomlar matematiğin tamamen bir sisteme oturtulması için çok önemlidir. Ayrıca Birkaç tane daha aksiyom örneği vereceksek şunu verebiliriz: \(a+(b+c)=b+(c+a)\) Bu çok absürt gelebilir, fakat bu bir aksiyomdur. Evet; 20 yüzyıldan önce matematikçiler, bunları biliyordu fakat genişleyen matematik dünyasında ortak bir temel gereklilik değil adeta bir zorunluluktu. Fakat bir de şöyle düşünün, evet; \(a+(b+c)=b+(c+a)\) eşitliğini her zaman biliyoruz. Fakat bunu nasıl kanıtlayabilirsin? Matematikte bir şeye inanıyorsanız onu ya kanıtlamış olmanız gerekir ya da o şey salt aksiyomdur. Elinize kağıt kalem almaya çalışın ve \(a+(b+c)=b+(c+a)\) önermesini kanıtlamaya çalışın. Yapabildiniz mi? Sanmıyorum, fakat buna inanıyorsunuz; neden inanıyorsunuz? Buna sebep olan şey, yıllardır bu kurala çok fazla maruz kalmanız ve adeta bunu doğal bir şey olarak görmeniz. Fakat biraz düşünürseniz bunun neden böyle olduğunu çözemeyeceğinizi göreceksiniz. O halde bu şey bir aksiyom olmalı! Demek ki \(a+(b+c)=b+(c+a)\) önermesinin aksiyom olması önemlidir, kesinlikle zırva veya absürt değildir.
Matematikte görüp görebileceğiz her şeyin temeli bu aksiyomlardır, birkaç aksiyomu kullanarak bir teorem keşfederiz. Sonra o teoremle başka bir aksiyomu harmanlayarak yeni bir teorem ispatlarsınız. Sonra iki teoremle başka bir teorem, onunla diğerlerini harmanlayıp başka bir teorem; gibi gider. Matematiğin en karmaşık alanlarına bakın, mesela İntegraller! İntegrallerin izini bir tarihçi gibi dikkatlice takip ederseniz eninde sonunda en temel aksiyomlara ulaşırsınız. Gördünüz mü, sanki dev bir soy ağacı gibi!
Son Söz
Bu yazımda karıştırılan kavramlara açıklık getirmeye çalıştım. Herkesin anlayabileceği şekilde, örnekler vererek yazmaya çalıştım. Umarım beğenmişsinizdir. Eğer lütfen bir hatamız varsa bize ulaşınız ki amacımıza daha iyi hizmet edelim. Şimdilik bilimle, matematikle ve sağlıcakla kalın; bir dahaki yazılarda görüşmek üzere.
KAYNAKÇA
Fizik Yasaları Üzerine, Richard Feynman, Alfa Yayınları
Fermat’s Last Theorem, Simon Singh
Ted-ED, Youtube Kanalı
Numberphile, Youtube Kanalı






orumlar
Çok güzel bir yazı olmuş ellerinize sağlık beyler.
Tebrikler
Yazı çok iyi olmuş. Teorik ve karışık bir konu örnekler üzerinden gayet açıklayıcı bir şekilde anlatılmış. Şahsen en çok matematik-bilim farkları ve benzerlikleri hakkındaki bölümü beğendim.