Blaise Pascal, aydınlar dünyasında en çok yönlü insanlardan biridir. Kendisi matematik, fizik, felsefe ile uğraşmıştır. Pascal, olasılık kuramını çok ilerletmiştir, şu an bile hayatımızda bilmesek bile bize her gün öyle böyle işe yarayan Pascal Prensibini keşfetti. Kendisi dindar bir felsefeciydi, düşünceleriyle Jean-Jacques Rousseau gibi düşünürleri etkiledi[1].,
Pascal’ın Hayatı
Pascal, 19 Haziran 1623’te Fransa’nın Clermont-Ferrand kentinde dünyaya gelmiştir. Annesi, Pascal daha 3 yaşındayken ölmüştür. Pascal ile ailesi 1631’de Paris’e taşınmıştır. Bu arada Pascal’ın babası Étienne Pascal, Pascal doğduğunda vergi mahkemesinde hakimlik yapıyordu. Pascal’ın annesi öldüğünde Pascal’ın babası çocuklarının eğitimine çok önem verdi ve üzerine düştü.[1]

Pascal’ın babası, Pascal ilk önce dil öğrenmesi için eve matematik kitaplarının girmesini yasakladı. Ama bu Pascal’ın sadece merakı arttırdı. Bilmediği bir şey onun çok ilgisini çekiyordu.Fakat azimli sıçanın duvarı deleceği gibi Pascal da matematiği gizli gizli öğrendi ve kendini matematik konusunda çok yetenekli bir hale getirdi.
Babası sonradan, Öklid’in kitaplarını yasaklamış olmasına rağmen tabi ki de ona diş geçiremedi ve Paris’teki Mersenne’nin Akademisindeki konuşmalara katılmasına izin verdi. 1640’ta daha 19 yaşındayken konik kesitler üzerine makale yazdı. [2]
Pascal ve ailesi sımsıkı Roman Katolik Prensiplerine tutunuyorlardı. Pascal, babası 1646’da ölünce daha da dindar hale geldi ve din üzerine düşündü. Bu düşüncüleri, kendinden sonra gelen filozofları etkiledi. Tabi ki hayatında daha olan çok şey var. Biz sadece kısa bir özet geçtik. Şimdi icatlarına, fikirlerine gelelim.
Olasılık Kuramına Katkıları
Kumar, para, tahta oyunları, zarlar insanlık tarihi kadar eskidir. Olasılık kuramı da öyle denilebilir. Fakat bu yanlıştır. Olasılık ne kadar bir insanın bir olay sonucunda isteyip istemediği şeyler (Mesela zar atıyorum, 6 gelsin istiyorum diğer rakamlar gelmesin istiyorum) olmasına rağmen insanlar bunları pek hesap etmemişlerdir.
İlk olasılık hesabı 1550 tarihinde Cardan tarafından yapılmıştır. Cardan bir zarın atılıp sonucun olasılıklarını içeren bir yazı yazmıştır. Yazı sonraki tarihlerde bulunmuş ve ilk olasılık hesabı diye tarihe geçmiştir. [3]

Bundan sonra olasılığın gelişmesi, büyük çoğunlukla Fermat ve Pascal’ın çabalarıyla olmuştur. Chevalier de Mere‘nin 1654’te Pascal’la paylaştığı bir kumar sorusuyla uğraşan Fermat ve Pascal, olasılığın en temelini oluşturdular. Matematik tarihinde bu ikili olasılığın “babası” sayılmaktadır. Ayrıca bu ikilinin mektuplaşmaları ünlüdür ve insanın gözünü gerçekten etkileyen mektup dizisidir, birazcık araştırmayla bu mektuplara ulaşabilirsiniz. [4]

Ayrıca Pascal, binom açılımlarını ve Ömer Hayyam üçgeninin uygulanabirliğini arttırmıştı. Halihazırda biz Pascal Üçgeni olarak biliriz ama aslında Hayyam Üçgenidir. Pascal’dan önce bunu keşfeden matematikçiler olmuştur. Fakat Pascal bunun uygulanabirliğini arttırmıştır.
Pascaline
Bunun yanında Pascal, babasının işlerini kolaylaştırması için o yıllarda gelişmiş sayılabilecek bir hesap makinesi icat etti.

Pascal’ın Fizik Yetenekleri de Kuvvetliydi
Pascal, 1640’ların sonunda fizikle alakalı deneylerine odaklanmıştı. Pascal, Galileo ve Torricelli’nin (Barometreyi ve hava basıncınının sayısal değerini keşfeden bilim insanı) teorilerini test ediyordu. Bunu yapmak için cıva barometresi ile atmosfer basıncı üzerine deneyler yapıyordu.
Bu deneyler sırasında şırınga ve hidrolik presi keşfetti. Bilimdeki adıyla Pascal Prensibi. Su dolu kapalı bir konteyner düşünün. Pascal Prensibine göre konteynerin bir tarafındaki basınç değişimi konteynerin her tarafında eşit ve kayıp olmayacak şekilde iletilecek. Nitekim de bu böyledir.
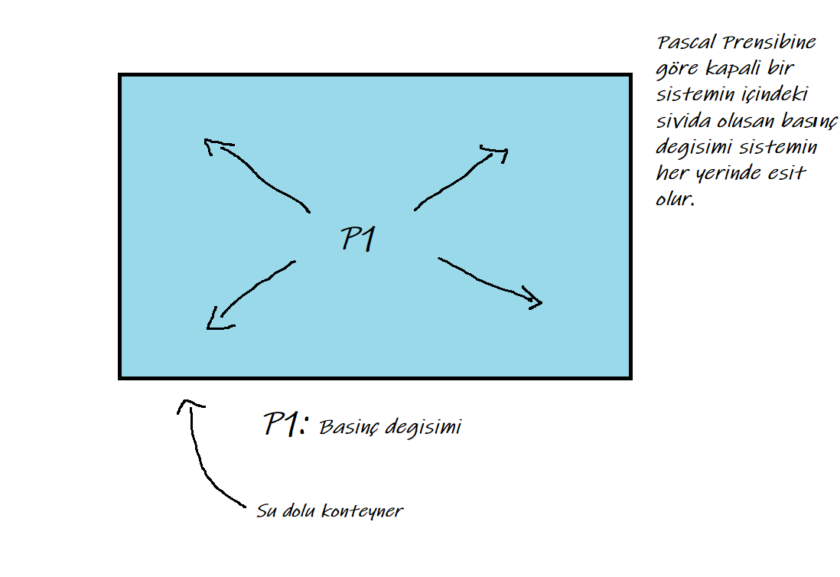
Hidrolik Pres ve su cenderesi fikri de böyledir.
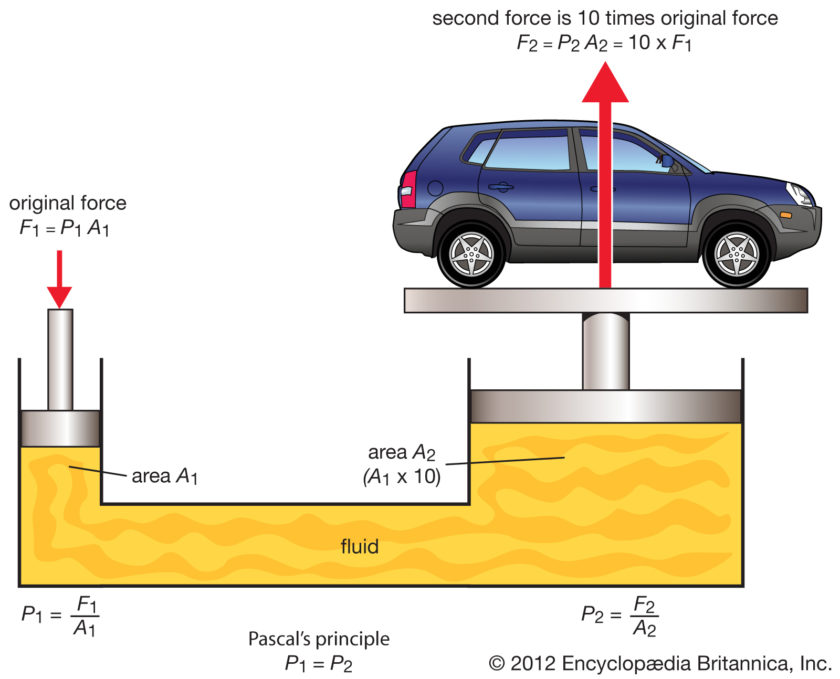
Şimdi bu resme baktığımızda olayı anlıyoruz. İlk olarak küçük pistondan F1 kuvvetini uygularız. Ardından piston hareket ederek su üzerinde basınç oluşturur. Bu da P1 olur. Tanım gereği (Basınç, santimetre başına düşen kuvvet veya ağırlık olduğu içi) P1=F1/A1. P1 basınç, F1 uyguladığımız 1 numaralı kuvvet, A1 ise 1. pistonun suya bakan kısmının yüzey alanı.
Devam edelim, su üzerinde oluşan basınç, her tarafa eşit şekilde dağılıyor. Bunun sonucunda, sıvıların sıkıştırılamaması (sıkıştırılır ama yok denecek kazar az) sayesinde 2 bölmede su üstündeki pistona basınç yapıyor. Dikkatinizi çekelim pistona etki eden basınç P1. Biz buna P2 diyelim, ama P1=P2. Burada da yine aynı şekilde P2=F2/A2. .F2, pistona uygulanan kuvvet; A2 ise ikinci pistonun suya bakan kısmının yüzey alanı.
Pascal Prensibine Bir Örnek
Yukarıda anlattıklarımızı herkes anlayabiliriz, önemli olan ana fikri anlamak. Bir örnek verelim, ilk önce değerlerimizi belirleyelim.
- 1. Pistona uygulanan kuvvet = 10 Newton
- 2. Pistonun suya bakan kısmının alanı = 1m^2 (1 metre kare)
- 3. Pistonun suya bakan kısmının alanı = 6m^2 (6 metre kare)
Hesaplar. Şimdi amacımız ilk olarak suya pompaladığımız basıncı hesaplayıp bulmak. Hemen yapalım, P1=F1/A1, P1=10/1=10N/m^2 Pascal. Kısacası 10 Pascal basınç
Bu basıncın diğer pistona etki eden basınca eşit olması gerekiyor. Bunu bir hesaplayalım. P1=P2 ise o zaman 10 Pascal = F2/6 olur. Denklemi çözersek F2=60 Newton gelir. Ne fazla ne eksik, muazzam! 10 Newton girdi kuvvet ile 60 Newton çıktı kuvveti elde ettik. Eğer sistemi güzelce oturtursanız elinizle dünyayı bile kaldırırsınız.
Hani Arşimet derdi ya: “Bana bir dayanak noktası verin dünyayı yerinden oynatıyım” sanki Pascal cevap vermiş: “Bana bir su cenderesi ve su verin Sagittarius A*yı Andromeda’ya fırlatayım” Tabi ki de böyle bir söz söylemedi. Bu son atlattığım hesapları anlamamanız normal, önemli olan buradaki ana fikri anlamak. Şimdi Pascal’ın diğer bir ilgi alanına geçelim: Felsefe!

Pascal’ın Felsefesi
Bir para atarsınız eğer para yeni basılmışsa yazı tura gelme olasılı neredeyse aynıdır. “Yazı gelirse 10 TL alacağım, tura gelirse 4 Tl vereceğim” diye bir oyun olsa bunu oynamamız mantıklı olurdu. Beklentimiz ise \(10*1/2-4*1/2=2,5 \) TL olur. Bu durumda oyunu oynamamız mantıklıdır. (Demin kullandığım şey olasılık kuramında bir uygulamadır, bilmenize gerek yok.)
Peki Tanrının var olup olmaması? Onunla bahse girmeye değer miydi? Pascal bunu düşünmüştü. Hadi geçelim.

Pascal ve ailesi, daha önce söylediğimiz üzere dini bütün ve dinine sımsıkı bağlı dindardı. Bunun yanında Pascal, insanlık için karamsar görüşlere sahipti. İnsanoğlunun cinsel isteklerine yenik düştüğünü, güvenilmez, paragöz olduğu gibi şeyler düşünüyordu. Fakat Pascal, eğer Tanrı’ya inancımızı kaybetmezsek insanoğlunun gene de bir şansının olacağını düşünüyordu.
Pascal’ın Hristiyan felsefesinin çoğunu 1670 yılında 39 yaşında erkenden ölmesinden sonra yayınlanan “Düşünceler” adlı kitabından anlıyoruz. Kitabın temel amacı belli: Hristiyanlığı savunmak.
Pascal, Jansenizm olarak bilinen din akımına katıldıktan sonra, pozitif bilimler yerine dini konular üzerinde yazmaya başladı. Janseistler alın yazısına yani kadere inanırlardı. Bunun yanında sert bir yaşamı benimserlerdi. Bir keresinde Pascal; kız kardeşini kendi çocuğuna sarıldığını gördüğünde kız kardeşine kızmıştı çünkü duyguların dışa vurulmasını sevmezdi.
Pascal, Tanrı’ya ulaşmanın akıl ve mantıkla olamayacağını, inancın kalpten gelmesini savunuyordu. Tanrı’nın elinin doğada görebileceğimize inanmıyordu mesela.
Şimdi Gelelim Blaise Pascal’ın Argümanına
Pascal, dinsiz olanların Hristiyanlığa inanmaları gerektiklerine ikna edilmesi gerektiğini savundu. Bunun için de zekice bir argüman geliştirdi.
Diyelim ki kumar oynayacaksınız. Kumarı, hem kazancınızı hem de kaybınızı belirleyerek oynarsınız. Mesela şu akıl karı değildir: 100 binde 1 ihtimalle 10 bin TL kazanacaksınız, öbür türlü 2000 TL kaybedeceksiniz. Evet, eğer çok şanslıysanız 10 bini kaparsınız ama kapmayıp elinizde patlama ihtimali de var. Ki bu çok yüksek ihtimalle.
Olasılık kuramının bir uygulaması olan beklenti ile bunu hesaplayalım. \(10000*1/100000-2000*99999/10000=~-20000\). Yani -20000 TL beklentimiz var. Bu olasılık kuramı için olağanüstü bir kayıp.
Pascal’ın argümanına göre Tanrı bahsi de böyleydi. Olasılıkları sıralayalım.

- Eğer Tanrı varsa:
- İnanıyorsan ve dini benimsediysen: çok iyi cennete gidersin
- İnanmıyorsan: cehenneme gidersin. Çok kötü bir sonuç!
- Eğer Tanrı yoksa:
- İnanıyorsan: Çok bir şey fark etmiyor ve bir kaybın olmuyor.
- İnanmıyorsan: Zaten inanmamışsın bir şey değişmiyor.
Bu olasılıklara baktığımızda inanmadığımızda zararlı çıktığımızı görürüz. Tanrının var olmadığını düşünerek yaşayabilirsiniz, ölümden sonra toprak olacağınıza da ,üstüne üstlük kilisede vakit bile geçirmenize gerek yok. Fakat bu Pascal’a göre büyük risk taşır.
Tanrı yoksa evet, inanmayanlar için sıkıntı yok amma velakin eğer varsa o zaman büyük sıkıntı. Cennete gitme hakkını kaçırmanın yanında sonsuza dek işkence göreceğiz cehennemde yaşayacaksınız, hayal edilebilecek en kötü sonuç. Fakat inanıyorsanız ve Tanrı varsa cennete gidersiniz, yoksa da size pek zararı dokunmaz.
Pascal’ın argümanı böyledir. Fakat burada bir kırık vardır. Eğer bir ateist bu yolla Hristiyan olursa bunun nedeni ateistin kalbinden geleceği için değil, basit bir olasılık hesabı yaptığındandır.
Bu dinler için büyük sorundur keza dinlerde en büyük temel kalple ve içten bir şekilde dine inanmaktır. Blaise Pascal’ın argümanı bunu başaramıyor. Ek bir bilgi olarak şu yazımızda bahsettiğimiz gibi filozoflar argümanlarını desteklemek için matematikten yararlanmışlardır: İlk Çağlardan Bugüne Matematik Dersleri: Matematik nasıl ortaya çıktı?.[6]
Son söz
Bu yazıyı yazmam nedense çok uzun süre aldı. Pazar Akşamından beri her akşam yazıyorum ve anca bitti. Yazı bence çok güzel ve bilgilendirici oldu. Sağlıcakla kalın!
Kaynakça
1) https://www.britannica.com/biography/Blaise-Pascal
2) https://www.biography.com/scholar/blaise-pascal
3) http://www.math.utep.edu/Faculty/mleung/probabilityandstatistics/beg.html
4) http://www.math.utep.edu/Faculty/mleung/probabilityandstatistics/beg.html
5) https://www.york.ac.uk/depts/maths/histstat/pascal.pdf
Felsefe bölümü, 6)Felsefenin Kısa Tarihi, Blaise Pascal bölümü, Nigel Warburton.






orumlar
Pascalın tanrıya imanı bile matematiğin bir konusu olan olasılığa bağlaması aslında onun dini konulara yönelmesine rağmen inancını ispatlarken matematiksel argümana dayanması aklının bir köşesinde her zaman matematiğin olduğunu gösteriyor.39 yaşında ölmeseydi acaba insanlığa daha hangi teoriler armağan edecekti?Bir dini akıma katıldığından söz etmişsiniz bu Hristiyanlığın hangi mezhebidir acaba? Her zaman dindar bir Hristiyan olduğu düşünülürse acaba matematiği felsefeyi dinini yaymak tanrı inancını kanıtlamak için mı öğrendi gibi sorular aklıma gelmektedir.