Ön söz:
Kuantum ilkelerinin anlaşılması çok zordur. Çünkü günlük hayatta karşılaştığımız şeyler değillerdir. Hareket gibi somut kavramları günlük hayatta deneyimleyebiliyoruz. Bu da konuyu daha kolay anlamamıza sebep oluyor. Fakat iş kuantum ilkelerine gelince bunları günlük hayatta doğrudan deneyimlemiyoruz. O yüzden bu konuyu anlamak zor oluyor. O yüzden bunu anlatmak için buradayız.
Werner Heisenberg’in ufak bir biyografisi:
Heisenberg 20. Yüzyılın başlarında doğup 20. Yüzyılın son çeyreğine birkaç sene kala dünyadan ayrıldı. Kendisi kendisi gibi birçok bilim insanıyla çalıştı. Söz gelimi David Hilbert, Niels Bohr ve Max Born gibi kişilerle çalıştı. Kendi bir çok bilimsel makalenin yazılmasında yardımcı oldu. Kendisinin de çok makalesi vardır fakat içlerinden en bilineni kendi ismiyle de anılan Heisenberg Belirsizli İlkesidir ki bu bilim dünyasını derinden sarmıştır ve kuantum kuramı için bir devrim sayılabilir. Kendisinin üniversitelerde öğretmenliği de vardır. O dönemin iyi üniversitelerde hocalık yapmıştır. Heisenberg, kült olmuş Einstein (Laf attığım yok Einstein de çok katkı yapmıştır bilime.) kadar bilinmez. Fakat bilim yapmak isteyenler kesinlikle bilmelidir. Heisenberg, Einstein’den daha önemsiz değildir. ikisi de bilime katkı yapmak için ellerinden geleni vermişlerdir.
Konuya girelim artık
Neyse şimdi konumuza dönelim. Heisenberg ilkesi kısaca bir parçacığın (ki bunlar çok küçüktür) aynı anda hem hızının, hem de konumunun aynı doğrulukla tanımlanamayacağını söyler? Ne ki şimdi bu? Şimdi bu demek ki, bir parçacığın hızını ne kadar doğru ölçmek istiyorsak konumunu o kadar kötü tutarlılıkla ölçeriz. Hızı çok iyi ölçmek istiyorsak konumu o kadar kötü ölçüyoruz. Veya tam tersi. Peki neden? Sadece olgularla yetinseydik “Bu taş yere düşecek” dediğimde Nobel Fizik almam gerekirdi. Fakat asıl önemli olan nedenlerle ilgilenmektir olguları herkes bilir. Mesela elma düşüyor da Ay neden düşmüyor? Şimdi de Heiseneberg’in Belirsizlik İlkesinin olgusunu bir kenara bırakalım ve neden böyle olduğunu düşünelim. Kolay, Orta ve Bilimsel olmak üzere üç tane argüman sunacağız ve her yönden bu ilkeyi anlamanızı sağlayacağız. Ayrıca bu konu hakkında da şu yazıyı önerebilirim: Bilim Nasıl Çalışır: Teori ve Kanun, Matematikle Farkı Bu yazı bilimin nasıl işlediğine dair size güzel bilgiler verebilir. Her neyse Hemen şuan basit bir argümanla başlayalım:
1)Basit argümanlar:
Öncelikle Belirsizlik İlkesi bir parçacığın hem hızının hem konumunun aynı anda aynı tutarlılıkta ölçülemeyeceğini ve birini ne kadar iyi tutarlılıkla ölçmek istiyorsak diğerini o kadar kötü tutarlılıkla ölçeriz. Şimdi bunun bir örnekle açıklamaya çalışalım. (İlk önce bu düşünce deneyinde boyutları cm olarak alacağız) İki küpümüz olsun. birinin boyutları 4*4*4. Yani hacmi (varsayımsal olarak) 64 cm3. İkinci bir küpümüz daha olsun. Onun da boyutları 6*6*6 olsun. Gene hacmi 216 cm3 olacaktır. Şimdi küçüklüğümüzde en az bir kere oynadığımız zıplayan topları düşünün. Bu toplar parçacıkları simgeleyecek. Bu topu odanızda bir fırlattığınızda her yere gitme ve yatağın, koltuğun altına kaçma ihtimali vardır, hey gidi günler be! Neyse konuya dönelim. İşte bu zıplayan topları kullanalım. Diyelim ki iki küpün her birine bir zıplayan top atıcı bağlı. İkisi de aynı hızla ve aynı prosedürlerle topu fırlatıyor. Şimdi topları fırlatalım ve sırasıyla küpleri ve zıplayan topları inceleyelim ve sonra iki küpü karşılaştıralım. Birinci küpten başlayalım. Birinci küp daha dar olduğu için zıplayan top kenarlara daha çok çarpmıştır ve tıpkı küçükken olduğu gibi muazzam bir hız kazanmıştır. Ama onun yanında küp dar olduğu için zıplayan topun konumunu daha kolay tespit edebiliriz. Çünkü gidebileceği yerler daha azdır. Yani hızdan feragat ederek konumu daha iyi bir tutarlılıkla ölçüyoruz. İkinci küpü inceleyelim şimdi. İkinci küp daha geniş olduğu için zıplayan top, daha az hızlanır ve bir kenardan diğer kenara giderken hız kaybeder değil mi sürtünme var sonuçta? Ama onun yanında küp geniş, konumunu kestirmemiz daha zor çünkü topun gidebileceği yer fazla. Yani hızı daha iyi kestirebiliriz fakat bunun yanında konumdan feragat ediyoruz. İşte bu. Hem hızı hem de konumu aynı tutarlılıkta ölçemedik. Bu tip deneylere düşünce deneyleri denir. Bu da basit bir örneğidir.
Şimdi de 2. argümanımıza geçelim. Bu argümanı anlaması biraz daha zordur fakat tabi ki de hala anlanabilir. Dilerseniz hemen konuya geçelim:
Şimdi gördüğümüz şeyler “klasik fizik” dediğimiz fizik kanunları çerçevesinde hareket eder, etkileşime girer vs vs. Eğer bir topu basketbol potasında attığımızda bazı matematiksel işlemlerle topun oraya kaç saniyede gideceğini, topun hızını, ivmesini bulabiliriz. Bir nebze geleceği “tahmin” ediyoruz. Yani klasik fizikte olaylar kesindir. Belirli formülleri vardır ve bunlar, bir gün yorulup çalışmaya bırakana kadar etkilidirler. Evden fırına gitmek gibidir. Belirli üç beş yol vardır oralardan gidersiniz yolunuz bellidir, ne kadar metre, km gideceğiniz, hangi hızla gideceğiniz bellidir ve ölçülebilir. Olasılıklar azdır. Ama iş çok küçük şeylerin fiziğine daha bilimsel adla mikro fiziğe daha da bilimsel adla da Kuantum Fiziğine gelirse o zaman işler her zamanki gibi karışır. Kuantum dünyası karmakarışıktır. Klasik fizik gibi değildir, konumuz da olan Heisenberg’in Belirsizlik İlkesi nedeniyle hız ve konumu tam olarak bilinemez. Yani şüpheci yaklaşılır “Pyrrhon” bunu ne severdin yalnız be! Neyse konuya dönelim. Benzetmemiz ise şudur:
Yine ekmek almaya gidiyoruz. Ama bu sefer işler klasik fizikte olduğu gibi değil. Diyelim yollarımız parçacıkları simgelesin. Evinizin yakınındaki fırınların birini işaretleyin. Bu parçacığın gitmesini istediğiniz yer. Ayrıca oraya gitmek için parçacığın bir sürü yolu vardır değil mi? Ne de olsa parçacığın hacmi atom bulutunun hacminden çok daha küçüktür. Şimdi bu parçacığın belirlenen yollardan atom bulutunun içindeki seçtiğimiz noktaya (fırına) gitmesini düşünün. Bunun yanında da parçacığın çok ama çok ama çok yüksek hızlarda olduğunu düşünün. Bu bir Airbus’un İçi boş bir Dünya’da rastgele dolaşarak bir noktanın üzerinden geçmesi gibidir. Yani bir parçacığın belirli bir noktaya gidip gitmeyeceği belirsizdir. Atom bulutunda da sonsuz (hmm…) tane nokta olduğuna göre parçacığın atom bulutunun herhangi bir yerinde olup olmaması belirsizdir. Burası biraz Schrödinger’in Kedisine bağlanıyor. Onu da sonra anlatalım. 2. Bölümde hızı ve konumu aynı anda aynı tutarlılıkta ölçemeyiz tezini açıklamadık. Bu bölümde daha çok atomdaki parçacıklarının konumlarının belirsiz, kendilerinin de belirsiz olduğunu göstermiş olduk. Bu argümanlar ilkeyi anlamaya katkı sağlayacaktır.
Belki biraz anlayamamış olabilirsiniz, fakat dert etmeyin normaldir. Tane tane okumaya çalışın ve sistematik bir şekilde ilerlemeye çalışın. Dilerseniz 3. argümanımıza da geçelim. Bu argümanın anlaması açıkçası biraz zordur. Ama denemekten zarar gelmez!
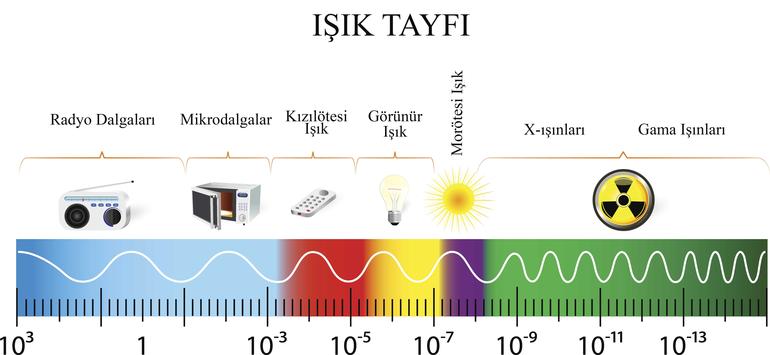
Klasik fizikte nesnelerin yerini ışık fotonları aracılığıyla görürüz. Foton diyince aklınız karışmasın, sadece günlük veya diğer ışıkların yapıtaşlarıdır. Ayrıca ışık fotonu diyince aklınıza sadece “gördüğümüz ışık” aklınıza gelmesin. Işığın farklı dalga boyları vardır. Ve bazılarını özel kameralarla vb. görürüz. Ayrıca klasik fizikte gördüğümüz şeylerin kolayca hızını, konumunu vb. ölçebiliriz. Kuantum fiziğinde ise gene bir parçacığın yerini ve konumunu tespit etmek için parçacığa bir ışık fotonu yollayıp ve bazı özel dedektörlerle bunu ölçeriz. Şimdi biz bir parçacığa nispeten güçsüz bir ışık fotonu olan görülebilir ışık fotonu atalım. Aynı parçacığa gene daha güçlü olan mor ötesi ışık fotonu yollayalım ve bunları karşılaştıralım. Görülebilir Işığın enerjisi, mor ötesi ışıktan daha azdır. Bundan yola çıkarak da parçacığa fırlattığımız görülebilir ışık fotonunun, parçacığı daha az hareketlendirdiğini görürüz çünkü görülebilir ışığın enerjisi mor ötesine göre daha düşüktür. Parçacıklar ise çok hassas olduklarından tek bir fotondan bile etkilenebilirler. Şimdi şuraya kadar baktığımızda şunu görürüz: G.I (Görülebilir ışık) fotonu, parçacığı M.I(Mor ötesi ışık) fotonundan daha az hareketlendirmiştir. Yani G.I ile ölçtüğümüz parçacıklar daha az hareket ederler ve onların hızını daha kolay ölçeriz. M.I fotonlarında da bunun tam tersi geçerlidir, onlar parçacıkları daha fazla harekete geçirip hızlarının tespit edilmesini daha zorlaştırır. Peki ya konumları? İşte bu da çok basit. G.I fotonları daha güçsüz olduğu için ışık tekrar yansırken güç kaybeder ve gözümüze yüksek tutarlılıkta bir konum olasılık çizelgesi gelmez. Fakat M.I fotonlarında ise fotonlar daha güçlü olduğu için parçacıktan daha güçlü bir şekilde yansırlar ve konumlarını daha iyi tespit ederler. Bu, gece yolda giderken minik bir el feneri ve kocaman askeri bir el fenerini karşılaştırmak gibi bir şeydir. Minik el feneri ile şeyleri daha az tespit edersiniz ışık gözünüze gelene kadar zayıflar da zayıflar. Askeri el feneri ise güçlüdür şeylerin yerini ve ne olduklarını kolayca tespit edebilirsiniz. Ayrıca olasılık demişken şu yazımızı önerebiliriz: Matematik ve Olasılığın İlginçliği ayrıca Kuantum Teorisi hakkında okumak isterseniz şu yazı tam sizin için: Kuantum Teorisi
Şimdi ise bunun teoride kullanım alanları.
Belirsizlik İlkesi sadece kağıt üstünde ve teoride kalmadı. Belirsizlik İlkesi; bazı fantastik, gerçekçi, bizi şaşırtan, korkutan teorilerin gerçekleştirilmesi yolunda önemli bir teorik ilerleme yaşattı. Mesela kütle çekim kuvveti her yerde aynı olmayabilir. Neden mi? Şimdi bir adam düşünün, bu adam bir tepe yapacak. Dümdüz toprak bir arazide. Adamın yapacağı tepe evreni simgelesin. Adam evi yapmak için yerden toprak alacak ve tepe oluşturacak. Adam uğraşmış uğraşmış tepeyi bitirmiş. Fakat bu tepeyi yaparken aynı zamanda yaptığı şeyin bir simetrik tersi ortaya çıkmıştır. Yani çukur. Buna kozmolojide negatif enerji deniyor işte. Çukurla tepenin hacmi aynı olacağına göre de negatif enerji miktarı=pozitif enerji miktarı ayrıca toplam negatif enerji miktarı+toplam pozitif enerji miktarı=0 olur. Enerji para gibidir. Hesabınızda, para varsa, parayı çeşitli yollarla dağıtabilirsiniz. Gelgelelim yakın geçmişe kadar inanılan klasik bilim yasalarına göre fazladan enerji kullanma olasılığına sahip değilsinizdir. Ancak yakın zamanda genel Görelelikten ayrı olarak evren resmimizde büyük bir devrim yaratan kuantum kuramı klasik yasaların hükmüne son verdi. Kuantum kuramı daha insancıldır ve bankadan fazladan para yani enerji çekmemize izin verir. Bunu evrenin bazı yerlerinde enerji yoğunluğunun pozitif, bazılarında ise negatif olması koşuluyla izin verir. Peki bu nasıl oluyor? Belirsizlik ilkesi. Belirsizlik ilkesi öğrendiğimiz üzere bir parçacığın aynı anda iyi tanımlanmış değerde olamayacağını söyler. Hızı ne kadar kesin ölçersek konum o kadar belirsizleşir, bu; tersi için de olur. Konuya dönersek boş uzay olarak düşündüğümüz şeyin içi tam sıfır olur dersek belirsizlik ilkesini ihlal etmiş oluruz. Bu alanlar tam sıfır olamaz. Eğer tam sıfır olsalardı değerleri hem konum hem de hız açısında iyi tanımlanmış olurdu. Değerleri sıfır noktasında iyi tanımlanmış konum ve sıfır noktasında iyi tanımlanmış bir hız görürdük. Nitekim bir yerde bir madde yoksa o maddenin oradaki hızı sıfırdır. Çünkü orada yoktur. Bu belirsizlik ilkesini ihlal eder. Bu bölgelerde boşluk dalgalanmaları denilen ve birdenbire ortaya çıkıp birbirinden ayrılıp ve sonra da birleşip birbirlerini ortadan kaldıran madde ve karşı-maddenin varlığını düşünebilirsiniz. (Madde ve anti-madde her saniye çıkıp birbirlerini yok eden 2 parçacıktır ve bu kanıtlanmıştır) Ki bu bir teori değildir ve ispatlanmıştır. Adı da Casimir Etkisidir. Ayrıca uzay boşluğunda da karanlık enerjinin var olduğunu düşünüyoruz. Bu teoriler hakkında da şu yazımızı okuyabilirsiniz: Karanlık Enerji Nedir, Ne Değildir? Son noktaya gelirsek karşı madde ve madde ayrılıp bir şekilde (Kara delikler, süpernovalar vb. sebebiyle) birbirlerinden uzaklaşabilirler ve bazı yerlerde pozitif ve negatif enerji yoğunluğu olabilir. Pozitif enerji yoğunluğu olan bölgelerde şuanki olduğu gibi cisimler, uzay zamanı kendi üzerine bükerler. Negatif enerji yoğunluğu olan bölgelerde de uzay zaman, tersine bükülerek kütle çekim kuvvetini, elektromanyetizmayı etkileyebilir. Aynı şekilde ise bu bölgelerde evrensel “sabit”ler, “elektromanyetizma ve kütleçekim denklemleri” bile farklı olabilir. Ayrıca Casimir Etkisi ve temelde Belirsizlik Etkisi sayesinde evrende hızlıca seyahat etmenin kısa bir yolunu bulmuş olabiliriz. Negatif enerji ile evreni bir şekilde ters yöne büküyoruz ve bir solucan deliği oluşturuyoruz. Belirsizlik ilkesi deyip geçmeyin bunlar gibi birçok teoriye katkısı dokundu.
Son söz
Bu işte. Zor değil. Sonuç olarak hem hızı hem konumu aynı tutarlılıkla ölçemeyiz. Biri ne kadar kesinliğe doğru giderse diğeri o kadar belirsizliğe gider. Son bölümlerde biraz zorlanmış olabilirsiniz ki bu gayet normaldir. Fizik babası Feynman’ın şu sözünü unutmayalım: “Hiç kimsenin kuantum kuramını anlamadığını rahatlıkla söyleyebilirim.” Sevgili okurlar, bu blog sayfasını çeşitli nedenlerde açtık. Elimizden geldiğince yazı yazmaya, misyonumuzu gerçekleştirmeye çalışıyoruz. Amaçlarımızdan birisi de ülkemizde bilimi yaymak ve ön yargıyı kaldırmak. Bu amacımıza sen de katkı sağlamak istiyorsan bu yazıyı paylaşabilirsin. Ayrıca biz amatör yazıcılarız. Bilimsel yanlışlarımız, yanlış tanımladığımız şeyler ve daha birçok hatamız olabilir. Lütfen bu gördüğünüz hataları bize iletiniz ki daha iyi bir yazar olalım.
Hoşçakalın.