Matematik koca bir binaysa bu binanın içinde kolonlar, tuğlalar, betonlar, tip tip çimentolar, kablolar, sigortalar, su boruları falan filan vardır. Bu materyallerin kendine has işlevleri vardır. Ve hepsi birbirini tamamlar. Her birinin doğası farklıdır, kendine ait uygulamaları vardır. Bugün biz matematiğin kolonları olan ve kabloları çimentoları ayakta tutan sayılardan bahsedeceğiz. Tabiri caizse tekrardan icat edeceğiz veya keşfedeceğiz 🙂

Sayılar nasıl ortaya çıktı?
Tabi ki de bir süper zeka çıkıp ben sayıyı buldum demedi. Sayıların ortaya çıkma süreci ihtiyaçlarımızdan doğmuştur. Aynı matematik gibi, zaten matematiğin doğuşu da buradan gelir. Bu arada lütfen şu yazımızı okumadıysanız mutlaka okuyun: İlk Çağlardan Bugüne Matematik Dersleri: Matematik nasıl ortaya çıktı?
Bazı eski insanlar direkt olarak sayı kullanmaktansa her bir objenin yerine geçen çizgiler, taşlar gibi objeler kullandılar. Fakat bu yöntem büyük sayıları nitelemekte başarılı değildi. Bunun yerine milletler bazı “özel” objeleri daha büyük sayılara karşılık gelecek şekilde ayarladılar.
Mesela Antik Mısır sayı sisteminde bir çeşit halat 100’ü, lotus bitkisi ise 1000’i temsil ediyordu. Bunun nedeni daha büyük sayıları da temsil edebilmek.
Fakat insan sürekli gelişen bir varlık olduğundan daha fazla dal ortaya çıktı ve daha etkili sayı sistemleri gerekiyordu. İnsanların takas edebilmeleri için takas edilecek şeylerin sayısal değerlerini bilmelerini gerekiyordu. Mesela 5 elma karşılığında 20 ceviz.
Bu işlemler çok sayıya ulaştığında eski sayı sistemleri etkili olmuyordu. Bunlar hem karışık oluyordu hem o kadar da güvenli ve nesnel değillerdi. Daha rasyonel bir ölçüm stili gerekiyordu.

Mısırların sayılara tekabül eden simgeleri. Çubuk birin, topuk onun, halat yüzün, lotus bitkisi binin, parmak ise on binin yerini tutuyor.
46206 gibi fantastik sayıların yazılması gösterildiği üzerine çok karmaşık. Bunun yerine daha rasyonel tekniklere gerek vardı.
Bunun üzerine çeşitli milletler çeşitli sayı sistemleri kullandılar. Mesela Babilliler 60 tabanında sayı sistemi kullandılar. Bu o kadar temeldir ki zamanlarımızın 60’la bölünmesi buradan gelir.
Fakat Hindistan’da öyle bir icat yapıldı ki tüm dünyaya yayıldı. Hintli matematikçiler 10 tabanında sayıları icat ettiler. “İyi de bunun 8’lik veya 16’lık tabandan farkı ne” diye sorabilirsiniz. Bunun nedeni insanın 10 parmağının olmasıdır. 10’luk sistemin en büyük özelliği insanın kalem kağıt kullanmadan direkt olarak parmaklarıyla işlem yapabilmesiydi. Bu da günlük hayattaki insanlar için yetiyor da artıyordu bile.
Bunun yanında Sümerlerin 60’lı sayı sistemine bakacak olursak 10 parmaklı insanlara göre biraz karmaşıktır. Mesela bugünkü sayı sistemiyle 120, 60’lı sayı sisteminde 20’ye tekabül ediyordu.

Bazı kısımlardan daha kullanışlıydı. Ayrıca 60’lının kullanılmasının mantıklı sebepleri vardı. Mesela Babillilerden önce bölgede 10 ile 12 sayı sistemini kullanan ırklar vardı. Burası tek bir devlet ve ekonomi olduğunda insanlar kolaylık sağlaması için 10 ile 12’nin en küçük ortak katı olan 60 tabanını kullandılar.
Ayrıca 60’ın bölen sayısı çok fazlaydı ki bu da kolaylık sağlıyordu.
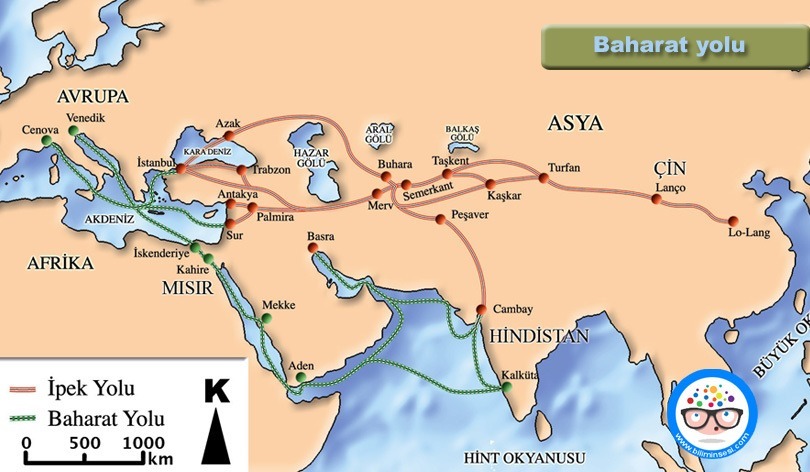
Fakat biz ne dersek diyelim her tabanın bir avantajı vardı. Dediğimiz gibi 10 tabanının yaygınlaşmasının sebebi 10 parmağımız olması diyebiliriz. Fakat bunun yanında bir de Baharat yolu etkisi var. Hindistan’da 10’lu taban kullanılmaya başlandığında tabi ki de ticaret bununla yapılacaktı. Bu yüzden yolun geçtiği yerlerde bu çok yaygınlaştı. Avrupa mesela.
Sıfırı kim keşfetti?
Sıfırın keşfi, farklı zamanlarda farklı milletlere denk gelir. Çinliler, Hintliler ve Türk-İslam bilim insanları 0’ı keşfetmişlerdir. Sıfır, sayıları hem büyütebiliyor hem de yokluk anlamına gelen bir sayı olabiliyordu. Hep 2 elma, ticaret gibi şeylerden bahsettik, ya yokluk olan bir durum olsa? Mesela adam beni kazıkladı 0 TL kazandım 2000 TL verdim. Sıfır, bu sayısal olarak yokluk elemanının yokluğunu giderdi.
Şimdi işin matematiksel kısmına geçelim.
Sıra işin matematiksel kısmında. Gerçekten, matematikte sayılar çok temeldir. Bu sayıları bilmeden matematik yapmayı bırakın günlük işlerinizi bile yapamazsınız.
Negatif Sayılara Kısa Bir Bakış
Negatif sayıların temel çıkış noktası şudur: Evimdeki çocuklar çok aç yemek yemeleri gerek ve benim 10 liram var. En ucuz yemek 15 TL, param yetmiyor ama illaki almam gerek. Alıyorum, ama 5 TL karşı tarafa borçlanıyorum.
Matematiksel notasyon olarak eskiden tabi ki de -5,-8,-300 gibi sayılar yoktu fakat pratikte borçlanma sistemi negatif sayılar üzerine kuruluydu. Az önceki örnekte 10 TL ile 15 TL’lik yemeği aldınız. 0 TL’niz değil -5 TL’niz kaldı. Hala param var diye sevinebilirsiniz. Negatif sayıların “belirli” notasyonla ortaya çıkması bankacılığın gelişmesi ve borç sisteminin sistematikleşmesidir.
Mesela asal sayılar, asal sayılarla tüm sayıları oluşturabilirsiniz. Biri bile. Tanıma göre bir, hiç tane asal sayının toplamıdır; evet hiç tane. \(4=2*2\)… \(6=3*2\)… \(35=7*5\)… \(36=2*2*3*3\).
Asal Sayılar
Asal sayılar belki de matematiği anlayabilmemiz için en önemli dallardan birisidir. Demin gösterdiğim gibi asal sayı dışındaki tüm sayılar belirli asal sayılar tarafından ve tek türlü yazılabilir. Bunun ispatını görmüştüm fakat hem uzun, hem anlaması zor öyle ki hala anlayamadım.
Asal Sayı Tanımı: Birden ve kendisinden başka sayıya bölünmeyen sayılara asal sayıdenir. Mesela 17, 23,3; nitekim bu sayılar sadece bire ve kendisine bölünür.
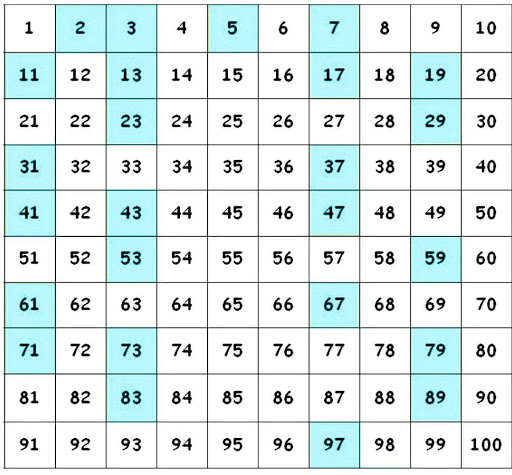
Hangi sayıların asal sayı olup olmadığı insanları her zaman meraklandırmıştır. Hatta 90’lı yıllarda çok büyük asal sayıları bulmak çok popüler olmuştur. Ha, sayı dediğimiz öyle yüz, bin değil. 25 bin rakamlı sayı mesela. Böyle büyüklükteki bir sayı kadar madeni parayı üst üste dizerseniz ve üstüne çıkarsanız yoklukta geziyor olacaksınızdır.
Kaç tane asal var?
Evet, sahiden, kaç tane asal var? İçgüdüleriniz sezgisel olarak buna sonsuz diyebilir. Nitekim öyledir, Öklid 3. yüzyılda bunu kanıtlamıştır. Kanıtı bugün dahi en şık ve basit kanıtlardan biri olarak geçer.
Sınırlı sayıda asalımız olsun. Bu asalların oluşturduğu grup şöyle olsun: 2,3,….,p. Yani en büyük asal sayı p olsun. Öklid bir kurnazlık yapar ve tüm bu sayıları çarpıp 1 ekler. Sayımız \(2*3*5*….*p+1\) olur. Sonuna eklediğimiz +1 bu sayının ne 2’ye, ne 3’e, ne listedeki tüm sayılara bölünmesini sağlar. Asal sayı dışındaki tüm sayılar asal sayıların çarpımı şeklinde yazılabilir
Fakat yukarıdaki sayı, asal sayıların çarpımı şeklinde yazılamadığından bu sayı bir asal sayıdır. Fakat biz demin en büyük asal sayı p demiştik ama ondan daha büyük bir asal sayı bulduk. Çelişki. İşlemlerimizde hata olmadığına göre varsayımımızda var. Demek ki asal sayılar sonlu değil, sonsuz. Gerçekten de asal sayı adeti sonsuzmuş! (Bu arada bu kanıtı anlayamayabilirsiniz, sıkıntı yok, önemli olan ana fikri anlamak.

Asal sayıların şifrelemedeki yolu: Asal sayılar, şifrelemede de çok kullanılır. Günümüzde RSA metoduyla dosyaları şifreleriz, bu da asal sayıları kullanır. Bu kullanımım temel prensibi çok büyük sayıların asal sayılarına ayrılmasının çok zor olmasıdır.
İki tane büyük asal sayıyı alırız ve çarparız. Kendimize özel bir anahtar oluşturmuş olduk. Bu böyle gider. Bu süreç hem karmaşık hem de biraz uzundur. Ondan buraya yazmıyorum, küçük bir araştırmayla bulabilirsiniz.
Mersenne Sayıları
Asal sayı deyip de “Mersenne Sayıları”na değinmemek olmaz. a sayısı asal olacak şekilde \( 2^a-1 \) türündeki sayılara Mersenne Sayıları denir. Özel olmasının sebebi, eskiden tüm a değerlerine karşılık Mersenne Sayısının asal olacağıydı. Fakat a=11 alırsak asal bir Mersenne Sayısı çıkmaz.
Fermat Teoremi
Fermat 350 yıl önce bir kitabın kenarına şunu yazmıştır desek yalan olur çünkü Türkçe değil Fransızca yazmıştır: “Bu iddiam için kesinlikle muhteşem bir ispat buldum ancak bu sayfanın kenarı onu alamayacak kadar dar.“
Fermat’ın teoremine bakış atmadan geçemeyiz. Zira tarihte birçok kişi bu teoremi kanıtlamaya çalışmış ama başaramamışlardır. En son Andrew Wiles ve öğrencisi teoremi 160 sayfada kanıtlamışlardır. Kanıtlamak içinse son modem matematiksel fikirler kullanılmıştır.

Fermat bunu kanıtladığını aktarmıştır. Fakat çok yüksek ihtimalle kanıtı yanlıştır. Çünkü bu teoremi kanıtlamak için anlaması çok zor ve modern matematik kullanılmıştır. Zira Andrew Wiles’ın kanıtını anlayan sadece birkaç profesör vardı. Çok yüksek ihtimal Fermat bir düşünce hatasına düştü.
Neden \(0!=1, x^0=1\)ve\(x*0=0\) ?
Sahi neden? İlk olarak 0!’den başlayalım. Bunu şu yazımızda anlatmıştık: 0! Neden 1’e eşittir?. Gayet güzel bir yazıydı okumanızı tavsiye ederim. \(x^0=1\) ise şöyle: bir sayıyı 0 kere kendisiyle çarpıyorsunuz. Yani hiç kere. Bunun herhangi bir anlamı yok.
Bunun nedeni sadece tanım gereği olması. Biz öyle istiyoruz. Bizim öyle işimize geliyor, hesaplarımızı kolaylaştırıyor. Balina bir balıktır keza bu tartışmasızdır fakat matematik zihinseldir ve kuralları insan koyar. Buna rağmen \(0^0\) cebirde tanımsız, analizde 1 olarak kabul edilir; çünkü işimize gelir.
\(x*0\). Bu da öyledir. Bir sayıyı sıfırla çarpıp sonucu sıfır bulmak sayı sistemlerinin aksiyomlarındandır. Aksiyom, yani tartışmasız, ispata gerek olmadan kabul edilen önermelerdir. Bunları da insanlar belirler. Eğer işimize gelecek olsaydı \(x*1=0\) diyebilirdik. Ama işimize gelmez! İşimize geldiği gibi yani. Bu konu hakkında şu yazımızı tavsiye edebilirim: Bilim Nasıl Çalışır: Teori ve Kanun, Matematikle Farkı

Sayılar artık zihinsel!
18. yüzyılın sonlarına ve 19. yüzyıla kadar sayılar hep sezgisel olarak kullanıldı. Fakat bazı matematikçiler bunları daha soyutlaştırmak ve matematikleştirmek istediler. Mesela doğal sayıların aksiyomlarını oluşturdular. Mesela:
a. Verilen küme boş değildir. 1 adı verilen bir nesne içerir.

b. Her doğal sayı için onun ardılı denilen başka bir doğal sayı ve yalnızca bir doğal sayı vardır.
c. Ardılı 1 olan hiçbir doğal sayı yoktur.
d. İki doğal sayının ardılları eşitse, bu iki doğal sayı da eşittir.
e. Eğer herhangi bir doğal sayı topluluğu 1’i içeriyorsa, ve herhangi bir doğal sayıyı içerdiğinde o doğal sayının ardılını da içerme özelliği varsa, o zaman bu topluluk gerçekte bütün doğal sayıları içerir.
Mesela bunlar doğal sayıların aksiyomlarıdır. Gerçekten gördüğünüz gibi çok basittirler ama çok temeldirler. Bu dala analiz, bazı yönlerden de cebir denilebilir.

Sağda gördüğünüz Hilbert ve modern matematikçiler sağolsun sayılar daha çok matematikselleştirildi.
Aynı şekilde David Hilbert uzun mücadele sonucu Kümeler Kuramını da Georg Cantor’dan sonra iyice geliştirmiştir. Ayrıca “Sayılar Teorisi” adlı bir dal da ortaya çıkmıştır. Bir sayılar teorisini keşfettik gibi olmadı ama herkesin anlayabileceği şekilde, çok ayrıntıya girmeden, en iyisi böyle.
Sonsöz
Herkesin anlayabileceği, basit ve çok detaya girilmeyen bir yazı oldu. Bence çok güzel bir yazı oldu. Eğer bir eksiğimiz varsa lütfen bize ulaşın ve bildirin. Hoşça kalın.
Kaynakça
- Neden ve Nasıl: Matematik: Tudem Yayınları
- https://education.casio.co.uk/news/a-brief-history-of-numbers





