Geometri, eski çağlardan beri bilinmektedir. Kimi matematikçiler sadece meraklarından kimileri ise hocasının felsefi fikrini kanıtlamak istediklerinden geometriyi kullanmışlardır. Öyle ya da böyle, geometri doğadır bu yüzden de bunu inceleyen çok matematikçi olmuştur.
Milattan önce 5. ve 4. yüzyıllarda Parmenides diye bir filozof vardı. Bu filozof, evrende hiçbir şeyin ama hiçbir şeyin değişmediğini, hareketin ve buna benzer diğer şeylerin olmadığını düşünüyordu. Değişiyor gibi görsek de aslına bunun bir yanılsama olduğunu da düşünürdü.

Licence: CC BY-SA 3.0
Derslerine girenler arasında dönemin önemli filozofları da vardı. Parmenides’in fikirleri pek tutmadı. Hareket dediğimiz şey günlük hayatta her saniye deneyimlediğimiz bir şeydi fakat nasıl olur da hareket diye bir şey olmazdı?
Parmenides’in öğrencisi vardı ki onun hocasını savunmak için oluşturduğu düşünce deneyleri ve paradokslar yakın tarihe kadar çözülemedi ve akıllarda hep soru işareti olarak kaldı. O öğrencinin adı “Zenon”du.
Zenon’un Paradoksları
1) Aşil ve Kaplumbağa: Aşil yani Achilles, mitolojiye göre yarı tandırıdır. Annesi onu çocukken ayağından tutup ölümsüzlük ırmağına batırmıştır. Fakat Aşil’in ayak bileği ıslanmadığı için, Aşil o bölgeden ölümsüz değildir. O bölgeye de Aşil Tendonu denir.
Paris tanrısı ise Aşil’i o bölgeden vurarak öldürmüştür. Bu bilgi önemli, çünkü biraz sonra kullanacağız. Bu arada Aşil’in marifeti çok hızlı koşması, bu da aklınızı bir köşesinde dursun.
Şimdi geçelim paradoksa. Düz bir yol üzerinde Aşil ve Kaplumbağa var. Kaplumbağa Aşil’den biraz ötede. Aşil, Kaplumbağa’yı yakalamak istiyor zaten kendisi de diyor:”Ben çok hızlı koşarım zaten, bir kaplumbağayı yakalamak da ne var?” (!)
Aşil başlıyor, aynı anda kaplumbağa da başlıyor. Aşil, Kablumbağa’nın ilk bulunduğu yere ulaşıyor. Fakat bakıyor ki kaplumbağa biraz daha öteye gitmiş, ne de olsa o da hareket ediyor. Aşil harekete devam ediyor, kaplumbağanın olduğu yere gitti yine. Fakat yine kaplumbağa o süre zarfında daha ileriye gitmiş.
Böyle böyle Aşil hiçbir zaman kaplumbağayı yakalayamıyor. Evet çok hızlı olan tanrı kaplumbağayı yakalayamıyor. Çok ilginç.
Eğer Aşil kaplumbağayı yakalıyorsa bu bir aldatmacadır, size öyle gelir; Aşil kaplumbağayı yakalayamaz!
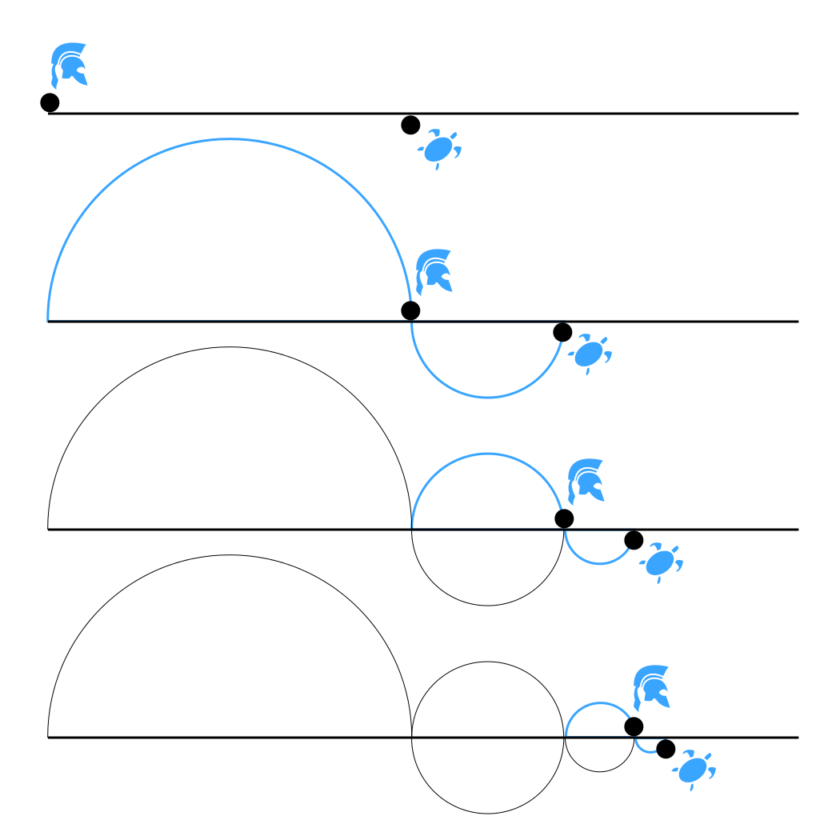
Aşil Kaplumbağanın konumuna gidiyor fakat kaplumbağa ilerliyor yine Aşil, kaplumbağanın bulunduğu yere gidiyor ama kaplumbağa daha da ilerlemiş oluyor. Yani kaplumbağaya hiç yetişemiyor
Licence CC: CC BY-SA 4.0
2)Yarısının yarısının yarısının yarısın…
Böyle bir yolumuz olduğunu düşünelim. Aşil, A noktasından B yani bitiş noktasına girmek istiyor. Fakat ufak bir problem var.
Aşil’in bitiş noktasına varabilmesi için ilk önce yolun yarısını gitmesi gerek. Sonra kalan yolun yarısını sonra kalan yolun yarısını, onun da yarısını ve böyle böyle hiç bir zaman varamayacak. Fakat B’nin burnunun dibine girecek.
Derler ya; Türkler, Viyana’nın kapılarına dayandı aynı onun gibi, burnunun dibindeyiz ama alamıyoruz, varamıyoruz.
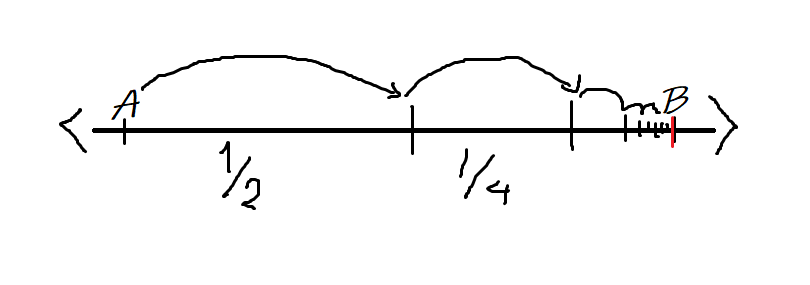
Dünya’nın belki de en hızlı varlığı Aşil, A’dan B’ye bile varamadı! Fakat düşündüğümüzde Aşil daha yerinden bile hareket etmedi. Çünkü Aşil B’Ye ulaşmak için kullanacağı 1/2’lik mesefeyi gidebilmesi için ilk olarak onun yarısına sonra ona gidebilmek için o yolun yarısına…. böylece yerinden sadece sıfır virgül bilmem kaç adım atabilecek.
Bu sefer, Dünya’nın en hızlı varlığı Aşil’in yerinden bile hareket edemediğini görüyoruz! Şunu söylesem nasıl olur Aşil ölmedi: Paris’in attığı okun Aşil’e ulaşabilmesi için Aşil’e ulaşacak okun eğrisinin mesafesinin yarısının yarısının… gitmesi gerek. Fakat gidemedi, gidemiyor, okun sivri ucu belki 5 santimetre daha gitse Aşil ölecek. Ama ölmüyor!
Hatta ve hatta ok yaydan bile çıkmıyor! Çünkü okun Aşil’in topuğuna gitmesi için gideceği 1/2’lik yolun yarısını ona gitmek için yine yarısını… gitmesi gerek. Yani “ok yaydan çıktı” diye bir atasözü yok yalan.
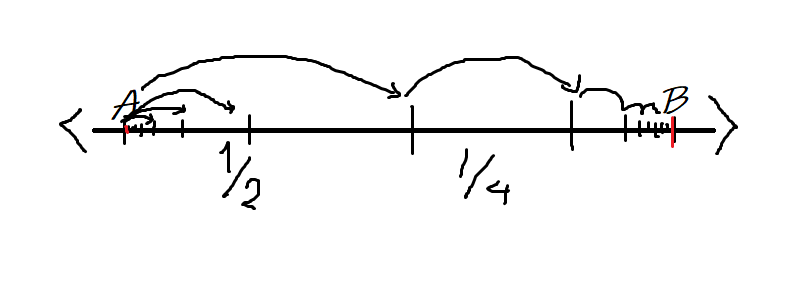
Hatta ve hatta direkt hareket diye bir şey yok! Paris’in attığı ok Aşil’e nasıl gidecek? Bir eğri çizecek değil mi? Ok havadayken zamanı durdur, ok nasıl? Duruyor. “Her” zamanda parçaları duran şey tamamen duruyordur! Yani hareketsizdir.
Gerçekten çok ilginç aynı zamanda akıl ve mantığı aşıyor mu dersiniz yoksa akıl mantık bu mu dersiniz bilemem. Fakat işin aslı şu ki bu paradoks ancak 19. yüzyıl civarında çözülmüştür.
Bunun çözümü de kalkülüsü barındırır. Çok masum bir problem gibi gözükse de dediğim gibi çok değişik bir problemdir. Ayrıca şuna dikkatinizi çekeyim: Şu yazımızda (İlk Çağlardan Bugüne Matematik Dersleri: Sayıların Doğası) demiştik ya bazı filozoflar, fikirlerini desteklemek için matematik kullanırlar. Matematiğin gelişimi de buradan çıkmıştır.
Aynı onun gibi Zenon da hocasının felsefi fikirlerini kanıtlamaya çalışmıştır. Bunu yaparken de matematiği kullanmıştır. Ayrıca dediğim gibi bu paradoksu çözmeye çalışan matematikçiler matematiğe çok katkıda bulunmuşlardır.
Bu bölüm için not: Bu konuyu tam anlayamadıysanız Barış Özcan’ın bu konudaki çok güzel görselleştirilmiş ve basit videosunu izlemenizi tavsiye ederim. Eğer meraklıysanız daha teorik ve matematiksel istiyorsanız şu videonun başlarını izleyebilirsiniz: https://www.youtube.com/watch?v=RLBhBwV3MPw&t=577s
Biraz Geometriye Geçelim Artık
Geometrinin tarihinden veya nasıl çıktığından bahsetmeyeceğim. Zira bundan 1. bölümde bahsetmiştik. Geometrinin adı geçmese bile 1. bölümde anlattığımız itibariyle geometri de ihtiyaçlardan çıkmıştır. Toprak parselleme mesela. Zaten Yunancada geometri, “toprak ölçümü” anlamına gelir.
Mısırlılar Piramitlerin Uzunluğunu Nasıl Ölçüyorlardı?
Mısırlılar, Piramitlerin boyunu ölçmek için çok zekice ve kullanışlı bir yöntem kullanıyorlardı. Bu sayede kendi amaçları doğrultusunda geometriyi geliştirmişlerdi.
Yöntem şuydu: Piramit’in yanına bir çubuk dikiyorlardı. Ve çubuğun gölgesini inceliyorlardı. Çubuk 1 metre, gölgesi 2 metre diyelim. Mısırlılar şöyle düşündü: Piramitin gölgesi 60 metre ise piramit 30 metredir.
Yani anlayacağınız çok basit bir şekilde belki de bilmeden üçgende benzerliği keşfettiler. Sonra bu işe meraklı olanlar bu işi ilerletti.
Bunun gibi geometri birçok şekilde bize yardımcı oldu. Eskiden piramidin ölçüsünü ölçemeye yarayan geometri şimdi bizi Ay’a, Mars’a götürüyor ve götürmeye devam edecek.
Düzlem Geometrisi ve Öklid
Yukarıda bahsettiğimiz meraklılardan biri Oklid olabilir. Öklid günümüzden yüzyıllar önce yaşamış olsa bile kendi icat ettiği düzlem, şekiller, tanımlar, aksiyomlar hala bugün kullanılıyor.
Öklid, geometrinin babasıdır desek yanlış değil son derece doğru olur. Zira kendisi geometrinin temeli olan noktayı, uzayı, açıyı, üçgeni vb. tanımlamıştır. Fakat bahsettiğimiz şeyler zihinseldir, buna dikkat çekelim. Öklid’in tanımladığı nokta sonsuz küçük, alanı olmayan bir noktaydı.

O yüzden Öklid’in tanımladığı nokta, doğru gibi şeyler hep zihinseldir. Daire de öyledir mesela. Tam olarak Pi oranına uygun olarak daireyi çizemeyiz, çünkü Pi sayısı irrasyonel bir sayıdır. O yüzden mükemmel daire sadece beynimizdedir, bu arada bu düşünceler idealistlere materyalistlere karşı çok güçlü koz vermiştir.
Öklid’in bu buluşlarını 13 ciltlik Elemanlar adlı kitabında sergilemiştir. Bu kitap hayati öneme sahiptir.
Öklid’in en temel aksiyomu: Paralellik aksiyomu
Bu aksiyom sayesinde geometriyle alakalı bir çok teoremi kanıtlayabilir Paralellik Aksiyomu: Bir noktadan başka bir nokta üzerindeki doğruya sadece bir tane doğru çizilebilir. Elinize kağıt kalem alıp bunu inceleyebilirsiniz, biz ise şu resimde gösterelim.
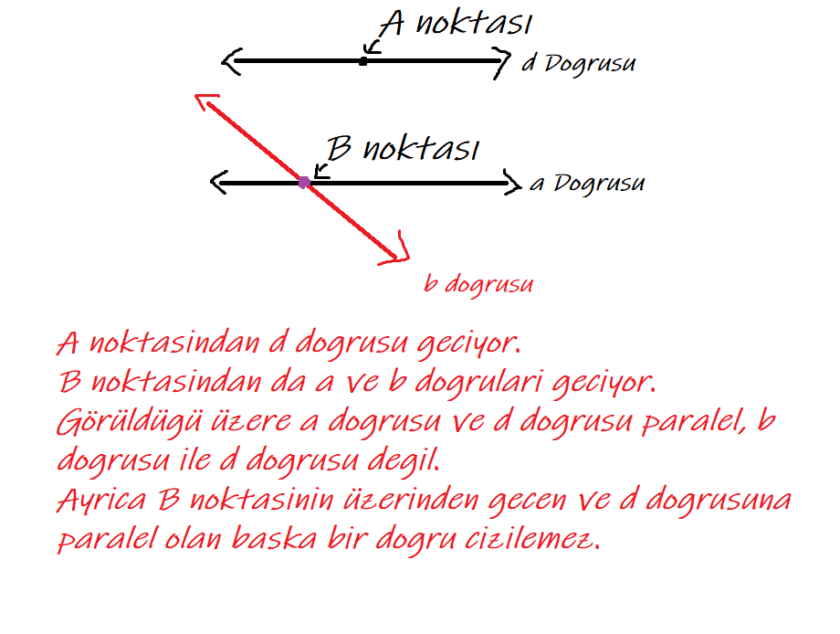
Şimdi gelin bu aksiyomla hemen bir teorem kanıtlayalım: Teorem: Üçgenin iç açıları toplamı 180 derecedir. Bunun neden olduğunu hiç merak ettiniz mi? Burada ilk okulda öyle öğrendim diye bir şey yok. Halbuki bunun kanıtı çok basittitir. Fakat kendimin çizim becerilerinin çok kötü olduğundan buraya bir video bırakmak istiyorum. Ayrıca aksiyomlar hakkında daha fazla bilgi edinmek istiyorsanız şu yazı tam size göre: Bilim Nasıl Çalışır: Teori ve Kanun, Matematikle Farkı
Pisagor Bağıntısı
Pisagor Bağıntısı yine en temel geometrik teoremlerden birisidir. Bir dik üçgenin dik kenarları a,b eğik kenarı yani hipotenüsü de c olursa \(a^2+b^2=c^2\) olur.
Bu teorem bundan fazlasıdır ama. İspat olarak ise onlarca ispatı vardır belki de. Yine bunları internetten bulabilirsiniz.
Pisagor Bağıntısı ve Köklü Sayılar
Bir süre sonra matematikçiler bir kenar bir birim diğer kenarı da bir birim olan bir dik üçgende hipotenüsün garip bir sayıya denk geldiğini fark ettiler. Bu sayı herhangi bir doğal sayının karesi değildi!
Böylece matematiğe yeni bir sayı dizisi katılmış oldu. Sonraki matematikçiler bunları kök simgesi gibi şeylerle simgelediler.
Arşimet Pi Sayısını Nasıl Hesapladı?
Arşimet kendi zamanına göre mükemmel diyebileceğimiz bir Pi sayısı hesabı yaptı. Hesap gerçek Pi sayısına çok yakındı peki bunu nasıl yaptı?

Gözünüzü kapatın ve kağıda rastgele, düzensiz, belirli bir şekli olmayan bir şekil çizin. Mesela benim şeklim tamamen eğrilerden oluşuyor ve alanını hesaplama yolumuz yok. Normal yollarla yani.
Bu şeklin alanını hesaplamak istersek nasıl hesaplayabilirdik? Aslında cevap basit: şeklin içine kareler yerleştirirdik. Sonra tüm bu karelerin alanını toplardık. Fakat fark ettiyseniz bazı yerlerde kareler şeklin dışına taşıyor. Bunu engellemek için ise daha küçük kareler kullanırdık.
Yani bu şekilde düzensiz bir şeklin alanını içine çok küçük kareler koyup tüm şekli kaplamalarını sağlarsak sonra da karelerin alanını toplarsak şeklin alanını bulmuş oluruz. Bu düşünce deneyi kalkülüsün de çıkış noktasıdır. Onu da başka bir zaman anlatırız.
Neyse Arşimet de bunun gibi düşündü. Daire o kadar da düzenli bir şekil değildi, kare göre mesela. Kare gibi alanını bulmak kolay değildi. Zira karede iki kenarı çarpıyorsunuz ve alana ulaşıyorsunuz, dikdörtgen ve üçgende de böyle.
Arşimet zamanında ve öncesinde Pi sayısının varlığı zaten biliniyordu. Değişik matematikçiler bunun değerini bulmak istiyordu. Arşimet de şöyle yaptı: az önce bahsettiğimiz şekli kareler ile doldurma fikrini uyguladı.
Bir dairenin içini çokgenlerle doldurdu. Şunu demek istiyorum çokgenin köşeleri dairenin kenarına teyetti.
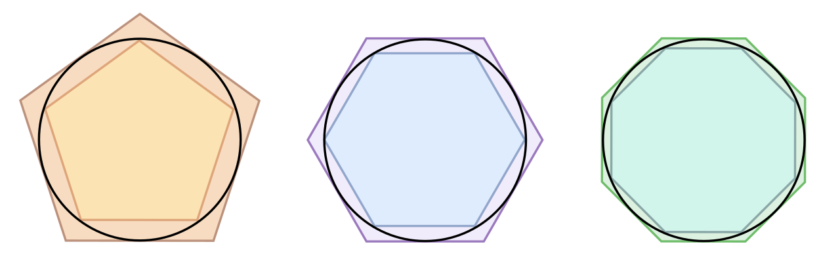
Şimdi yukarıdaki resme bakın. Siyah kenarlı şekil bir daire. Ve gördüğünüz üzere ilk şekilde dairenin kenarlarına, beşgenin köşeleri teğet olacak şekilde beşgen yerleştirilmiş. Sonra altıgen ondan sonra da sekizgen yerleştirilmiş, aynı şeyler dairenin dışarısından da yapılmış.
Baktığımızda çokgenlerin kenarı, dairenin kenarının şekline ve uzunluğa çok yaklaşıyor. Eğer ilk şekilde, dairenin içinde olan beşgenin alanına hesaplarsak değeri dairenin alanına az çok benzeyen bir değer buluruz. Fakat aynı şeyi en sağdaki şekil için yaparsak dairenin alanına çok yaklaşırız.
Arşimet böyle böyle devam ederek dairenin içine doksan altıgen yerleştirdi ve bu çokgenin alanını hesapladı. Bu şekilde Pi’ye çok yaklaştı. Size burada Arşimet’in hesaplarını anlatamayacağım maalsef, ama bilmeniz gereken şeyler bunlar.
Kartezyen Koordinatlar ve Descartes
Descartes, çocukluğunda hastalığı dolayısıyla sabahları yatakta çok kalırdı. Böylece Descartes için bu alışkanlık büyüdüğünde de devam etmişti. Ama artık felsefi ve matematiksel problemler düşünüyordu.
Yine bir gün yataktayken odanın üst kısımlarında sinek uçmaya başlamış. Descartes de merak etmiş: “bu sineğin birim zamanda nerede olduğunu nasıl anlayabilirim?” Descartes de düşünürken Kartezyen Koordinat sistemini keşfetmiş.
Kartezyen Koordinat Sistemi derken demek istediğim şu: mesela duvarınız bir düzlem olsun. Duvara bir nokta çizdiniz ve bu noktanın nerede olduğunu merak ediyorsunuz. Babanızdan mezura istiyorsunuz ve ölçüyorsunuz: noktanız, 2 metre yukarıda 1,5 metre sağda.
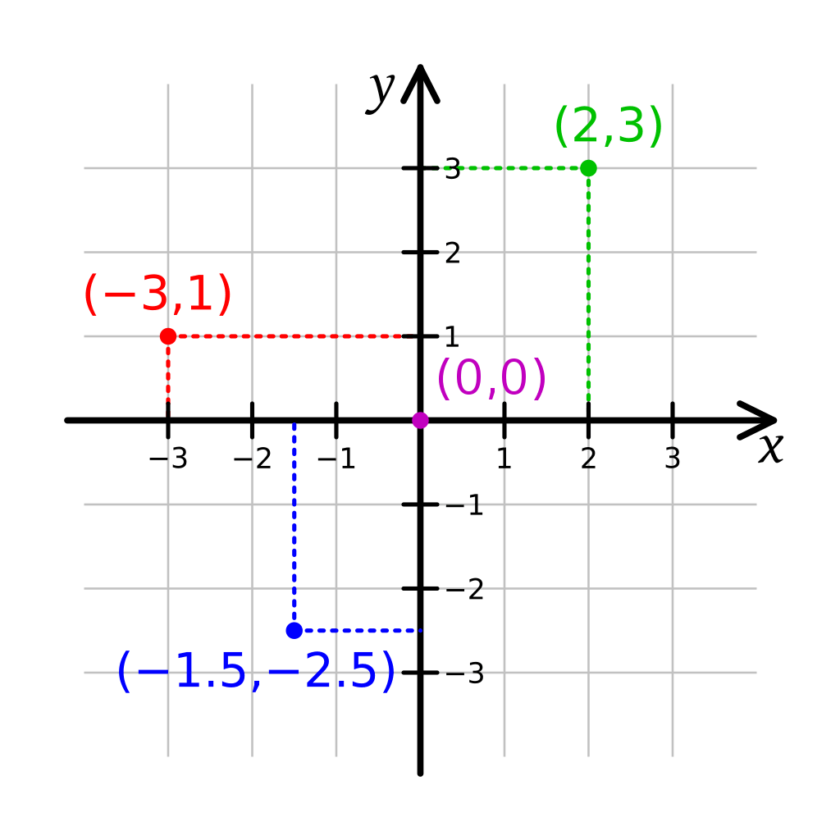
Bunun matematiksel hali kartezyen koordinat. Ne fazla ne eksik. Çok basit bir fikir olabilir ama çok kullanışlı. Ayrıca bu fikirden daha karmaşık fikirler gün yüzüne çıkmıştır. Nerede kullanabiliriz diye daha iyi akıl edenler artık düzlem değil de üç boyutlu uzay kullanmaya başlamışlar.
Yani artık bahsettiğimiz duvar değil, odanız. Şöyle: odanızın bir yerine iple top astınız. Bu topun nerede olduğunu göstermek için mezurayla ölçtükten sonra şöyle söylüyorsunuz: Kendime göre 3 metre önümde, 2 metre sağımda, 1 metre yukarımda. Yani artık 2 değer değil, 3 değer kullanıyorsunuz. Bu ise her şeyini 3. boyutta deneyimleyen varlıklar için muazzam bir şey!
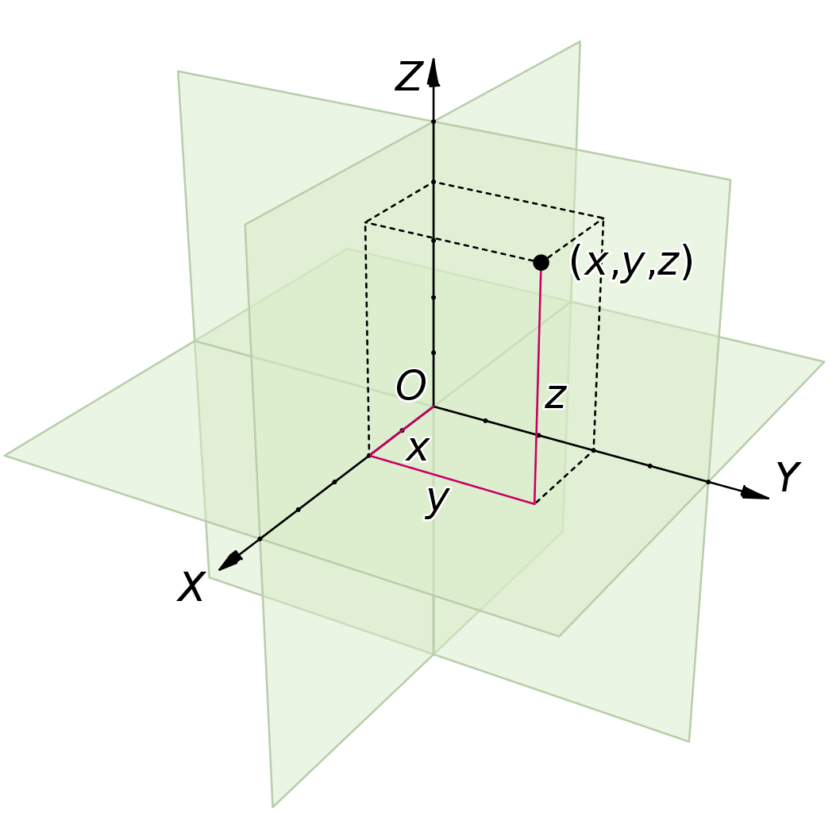
Öyle ki artık insanlar dünya üzerinde uçan uçakların anlık nerede olduklarını bulabiliyorlar çünkü kartezyen 3. boyutlu uzaydan türetilen bir şey var: coğrafya koordinatları, hani şöyle olanlar: 62 derece kuzey, 26 derece batı, dakika, saniye, bilmem ne bilmem ne. Bunların hepsi Descartes’in ortaya çıkardığı küçük bir kıvılcım sonucu.
Günlük Hayatımızda Geometri
Günlük hayatımızda geometri her yerdedir. Kitapların ölçüsü, telefonlar, trafiğin ayarlanması, yer şekillerinin gösterimi gibi şeyler. Trafikten örnek verecek olursak nerelerde trafik olacak, nereler daha yoğun gibi şeyleri ifade etmemizi sağlayan şey geometridir.

Licence: CC BY-SA 2.5
Son Söz
Herkesin anlayabileceği şekilde ancak bu kadar anlatabilirim. Her şeyi tam anlayamayabilirsiniz zaten önemli olan hepsini anlamak değil, önemli olan ana fikri anlayabilmek yani büyük resmi görmek. Eğer bir hatamız varsa lütfen bize ulaşın ve bildirin. Şimdilik hoşça kalın.
Kaynakça
1)Tudem Yayınları, Matematik, 3. bölüm.
2)https://www.youtube.com/watch?v=RLBhBwV3MPw&t=674s bu videonun başları.